notes/uni/mmme/2051_electromechanical_devices/ac_intro.md

author	date	title	tags	uuid	lecture_slides
Akbar Rahman	\today	MMME2051 // Introduction to Alternating Current (AC)	alternating_current ac	0c90c691-cbf8-43e9-bfa5-7b277c853151	./lecture_slides/MMME2051EMD_Lecture2B.pdf ./lecture_slides/MMME2051EMD_Lecture3A.pdf ./lecture_slides/MMME2051EMD_Lecture3B.pdf

This section builds on complex numbers.

Sinusoidal Waves

This module will be using the following format:

y(t) = A\cos(\omega t + \Phi)

where A is amplitude, \omega is frequency, \omega t + \Phi is phase angle, and \Phi is phase offset.

Explore the effects of changing the variables in Desmos

Phasor

• a phasor is a complex number that represents the initial position of a rotating vector
• use the amplitude (|V|) and phase offset (\Phi) of a cosine function
• for all AC steady state analysis (\omega is constant), these two variables are the only two needed

Example

For voltage v given by

v = 150 \cos (50t + 25)

it may be represented in the phasor form

150 \angle 25

Example

For current i given by

i = 10 \cos \left(50t -\frac{pi}{6}\right)

it may be represented in the phasor form

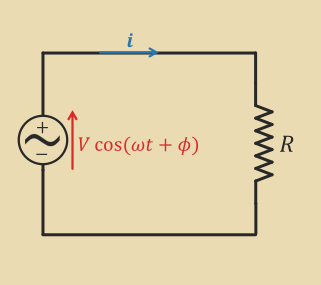
10 \angle \frac{pi}{6}

Phasors in Resistive Circuits

Convert all variables to phasors or to complex form

Apply KCL, KVL, Ohm's Law

\begin{align*} v &= iR \ V\angle \Phi = IR \angle\theta \ I \angle \theta = \frac VR \angle \Phi \end{align*}

Phasors in Inductive Circuit

Ohm's law generalised to incorporate complex resistance, reactance, X:

\begin{align*} v &= iX \ V\angle\Phi_v &= I\angle\Phi_iX \ &= I\angle\Phi_ij\omega L \ \frac{V}{j\omega L}\angle\Phi_v &= I\angle\Phi_i\ \frac{{V}\omega L}\angle\left(\Phi_v - \frac{\pi}{2}\right) &= I\angle\Phi_i \end{align*}

Power

Resistive Circuits

P_\text{avg} = V_\text{rms}I_\text{rms}

Inductive Circuits

P = \frac{V^2}{2\omega L}\sin{2\omega t}

Capacitive Circuits

P = \frac{\omega CV^2}{2}\sin{2\omega t}

Real Circuit (Resistive + Reactive)

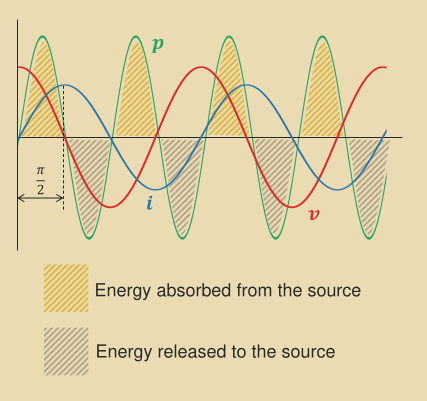
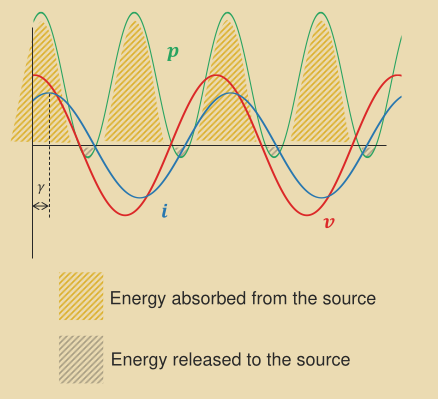
P = V_\text{RMS}I_\text{RMS}(\cos \gamma + \cos{(2\omega t + \gamma)}

P_\text{avg} = V_\text{RMS}I_\text{RMS}\cos \gamma

where \cos \gamma is the power factor (PF) and \gamma is phase deviation between voltage and current. The PF tells us what fraction of the current does useful work.

Apparent, Active, and Reactive Power

Apparent Power:

S = V_\text{RMS}I_\text{RMS}

• as power still flows losses still occur
• AC equipment is rated for apparent power as it handles both used and unused power

Active Power:

P = S\cos\gamma

• this is the real power transferred to the load

Reactive Power:

P = S\sin\gamma

A

Resonance

The inductive load of on a circuit is Z_C = \frac{1}{j\omega L}. If the frequency of the power supply matches \omega, you get resonance and the circuit becomes purely resistive so there is a sharp drop in impedance.