notes/uni/mmme/2051_electromechanical_devices/ac_power.md

author	date	title	tags	uuid	lecture_slides	exercise_sheets
Akbar Rahman	\today	MMME2051 // AC Power	ac alternating_current power	c269b4b7-7835-4b50-8d4f-ff5bc63a8a3d	./lecture_slides/MMME2051EMD_Lecture3B.pdf	./exercise_sheets/Exercise Sheet 4 - Power factor and three phase.pdf

This section builds on introduction to AC.

Definitions

• Phase voltage - voltage across any phase
• Line voltage - voltage between two live lines
• Phase current - current through any phase
• Line current - current through any live line

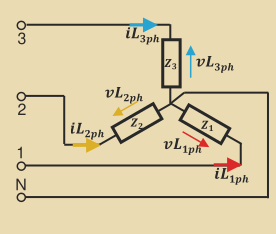
Three-Phase Load

P = \sqrt{3} V_lI_l\cos\gamma

• 3-phase devices (source and load) are usually balanced, meaning that the impedance in each phase is equal (Z_1 = Z_2 = Z_3).

• For loads, this means that the voltage across them are the same, apart from the phase angles:

  \begin{align*} v_{1N} = V\cos{2\pi ft} \ v_{2N} = V\cos{2\pi ft - \frac{2\pi}{3}} \ v_{3N} = V\cos{2\pi ft + \frac{2\pi}{3}} \end{align*}

• Balanced loads and sources ensure that line/phase currents have equal magnitudes and that the neutral current is 0

Star Load

|V_\text{line}| = \sqrt 3 |V_\text{phase}|

I_\text{line} = I_\text{phase}

Delta Load

|V_\text{line}| = |V_\text{phase}|

I_\text{line} = \sqrt 3 I_\text{phase}

Power Factor (PF)

\text{PF} = \cos{\gamma} = \cos{\left(\Phi_v-\Phi_i\right)}