3.9 KiB
Executable File
| author | date | title | tags | uuid | |||||
|---|---|---|---|---|---|---|---|---|---|
| Akbar Rahman | \today | MMME2053 // Fracture |
|
17315e63-3870-428b-b65d-a5d249768c05 |
Fracture
-
Consider the stress concentration factor (SCF) for an elliptical hole in a large, linear-elastic plate subjected to a remote, uniaxial stress
-
It can be shown that SCF can be expressed as:
K_t = \frac{\sigma_\text{max}^\text{el}}{\sigma_\text{nom}} = 1 + 2\frac{a}{b} -
Therefore as
b \rightarrow 0, the hole degenerates to a crack and $\frac ab \rightarrow \infty$\therefore K_t \rightarrow \infty, provided the material behaviour remains linear elastic
Basis of the Energy Approach to Fracture Mechanics
There are three modes of loading cases: K_\text{I}, K_\text{II}, K_\text{III}.
-
Generally, for geometries with finite boundaries,
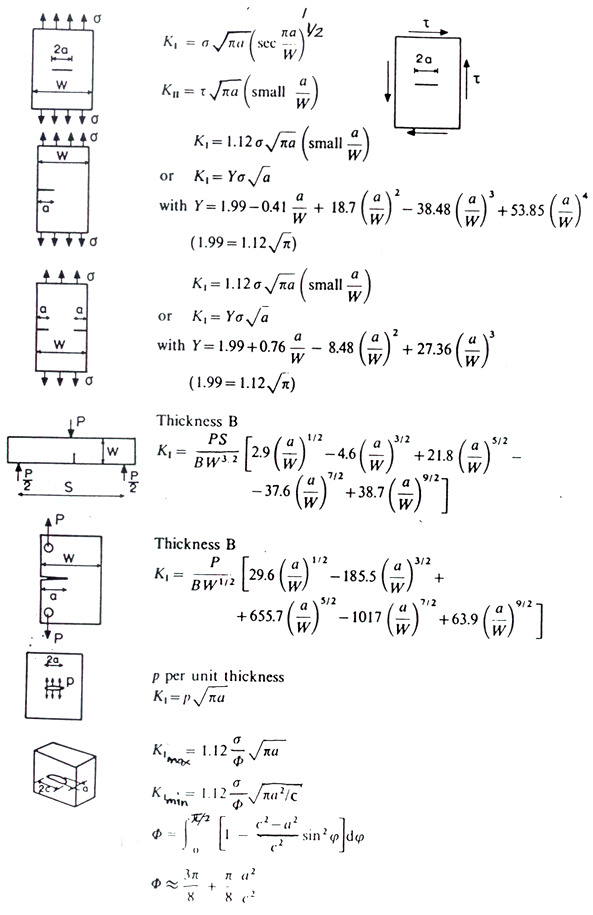
K_\text{I}is used:K_\text{I} = Y\sigma\sqrt{a\pi}where
Yis a function of the crack andais never mentioned in the slides (slide 6)TODO: find out what
Yandaare -
K_\text{I}is the Mode-1 stress-intensity factor which defined the magnitude of the elastic stress field in the vicinity of the crack tip -
K_\text{II}andK_\text{III}are similar -
The energy release release rate under mixed loading is given by
K_\text{total} = K_\text{I} + K_\text{II} + K_\text{III}
Typical Fracture Toughness Values
| Material | \sigma_y / Nm$^{-2}$ |
K_\text{Ic} / Nm$^{-1.5}$ |
|---|---|---|
| Mild steel | 220 | 140 to 200 |
| Pressure vessel steel (HY130) | 1700 | 170 |
| Aluminium Alloys | 100 to 600 | 45 to 23 |
| Cast Iron | 200 to 1000 | 20 to 6 |
Fatigue Crack Growth
-
for a wide range of conditions, there is a logarithmic linear between crack growth rate and intensity factor range during cyclic loading of cracked components
-
it allows crack growth to be modelled and estimated based on
- knowledge of crack and component geometry
- loading conditions
- empirical crack growth data
Considering a load cycle as shown in figure \ref{fig:p-vs-t} which gives rise to a load acting on a cracked body
-
The load range and crack geometry gives rise to a cyclic variation in stress intensity factor:
\Delta K = K_\text{max} - K_\text{min} -
Paris showed that subsequent crack growth can be modelled by following equation
\frac{\mathrm{d}a}{\mathrm{d}N} = C\Delta K^mwhere
Candmare empirically determined material constants. -
Fatigue crack growth data is often as
\log \frac{\mathrm{d}a}{\mathrm{d}N}against\log{\Delta K} -
Below
K_\text{th}, no observable crack growth occurs -
Region II shows a near linear relationship---this is the region which fail by fatigue failure spend most of their life
-
In region III rapid crack grown occurs and little life is involved
-
the fatigue crack growth life of the component can be obtained by integrating the Paris equation between the limits of the initial crack size and final crack size, given that you know the stress intensity factor
Typical Values for \Delta K_\text{th}, m, and \Delta K
| Material | \Delta K_\text{th} |
m |
\Delta K for \frac{\mathrm{d}a}{\mathrm{d}N} = 10^{-6} |
|---|---|---|---|
| Mild Steel | 4 to 7 | 3.3 | 6.2 |
| Stainless Steel | 4 to 6 | 3.1 | 6.3 |
| Aluminium | 1 to 2 | 2.9 | 2.9 |
| Copper | 1 to 3 | 3.9 | 4.3 |
| Brass | 2 to 4 | 4.0 | 4.3 to 66.3 |
| Nickel | 4 to 8 | 4.0 | 8.8 |