notes/uni/mmme/2053_mechanics_of_solids/asymmetrical_bending.md

author	date	title	tags	uuid
Akbar Rahman	\today	MMME2053 // Asymmetrical Beam Bending	mmme2053 beam_bending asymmetrical_beam_bending	7afb5f13-4d55-4e00-927a-5d622520d844

Procedure for Solving for Bending Stress and Neutral Axis Position in Asymmetrical Bending Problems

1. Determine the principal axes of the section (about which I_{xy}= 0)
2. Resolve bending moments onto these axes
3. Determine angle of neutral axis
4. Evaluate bending stress at any position in the section, such as extremes away from neutral axis, which give maximum bending stress

Worked Example

• [Worked Example 1 (PDF)](./worked_examples/MMME2053 AB WE1 Slides.pdf)
• [Worked Example 2 (PDF)](./worked_examples/MMME2053 AB WE2 Slides.pdf)

Product Moments of Area

To analyse asymmetrically loaded sections, we need the second moments of area I_{yy}, and $I_{xx}$ but we also need I_{xy}, the product moment of area:

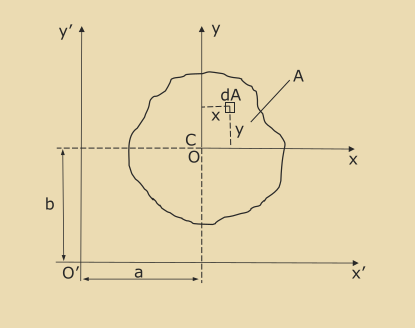
I_{xy} = \int_A xy \mathrm{d}A

Parallel Axis Theorem

The parallel axis theorem allows calculation of 2nd moments of area and product moments of area with respect to x' and y' axes:

\begin{align*} I_{x'x'} &= \int_A y'^2 \mathrm{d}A \ &= \int_A (y+b)^2 \mathrm{d}A \ &= \int_A (y^2 + b^2 + 2by) \mathrm{d}A \ \ I_{x'x'} &= I_{xx} + Ab^2 \end{align*}

Similarly you can get

\begin{align*} I_{y'y'} &= I_{yy} + Aa^2 \ I_{x'y'} &= I_{xy} + abA \end{align*}

Principal Axes and Principal 2nd Moments of Area

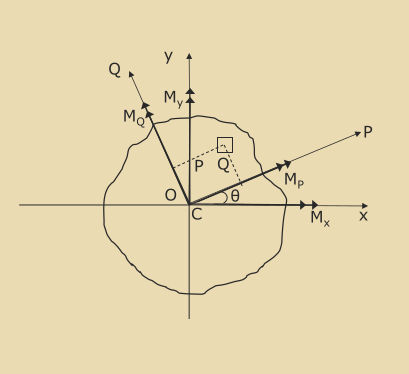
Once the second moments of area and product moments are found, they can be used to plot a Mohr's circle where:

• Point A is plotted at (I_{xx}, I_{xy})

• Point B is plotted at (I_{yy}, -I_{xy})

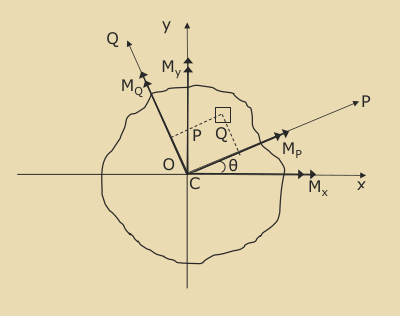
• Points P and Q show the positions of the principal 2nd moments of area, I_p, and I_q.

• \theta is the angular position e of the principal axes with respect to the $x$-y axes

  The principal axes are the axes where the product moment of area is 0.

C = \frac{I_{xx} + I_{yy}}{2}

R = \sqrt{\left(\frac{I_{xx}-I_{yy}}{2}\right)^2 + I_{xy}^2}

I_p = C + R

I_q = C - R

\sin{2\theta} = \frac{I_{xy}}{R}

Analyse Bending of a Beam with Asymmetric Section by Resolving Bending Moments onto Principal Axes

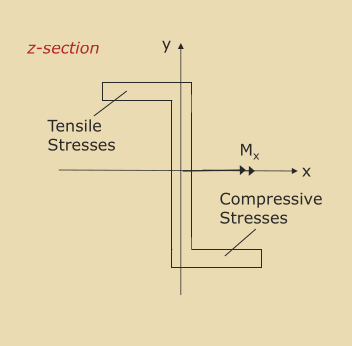
If a bending moment, M_x is applied about the x-axis only, then the stress in the flanges will cause bending to takeplace about both x and y axes. This is a consequence of I_{xy} \neq 0.

To avoid this moment coupling effect, it is usually convenient to solve bending problems by considering bending about the principal axes, for which I_{xy} = 0.

Resolving onto Principal Axes

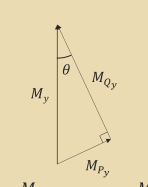
If bending moments M_x and M_y are applied about the x and y axes respectively, these can be resolved onto the principal axes, P and Q:

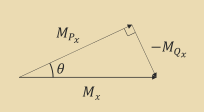
\begin{align*} \cos\theta &= \frac{M_{P_x}}{M_x} \rightarrow M_{P_x} = M_x\cos\theta\ \sin\theta &= \frac{-M_{Q_x}}{M_x} \rightarrow M_{Q_x} = -M_x\sin\theta\ \end{align*}

Similarly we get:

\begin{align*} M_{P_y} = M_y\sin\theta\ M_{Q_y} = M_y\cos\theta \end{align*}

Therefore:

\begin{align*} M_P = M_{P_x} + M_{P_y} = M_x\cos\theta + M_y\sin\theta \ M_Q = M_{Q_x} + M_{Q_y} = -M_x\sin\theta + M_y\cos\theta \end{align*}

Bending Stress at Position (P, Q)

\sigma = \frac{M_PQ}{I_P} - \frac{M_QP}{I_Q}

Note the -ve sign, as a positive stress results in a -ve moment about the y-axis.

Position of the Neutral Axis

The neutral axis is where \sigma = 0:

\begin{align*} \frac{M_PQ}{I_P} &= \frac{M_QP}{I_Q} \ \frac Q P &= \frac{M_QI_P}{M_PI_Q} \ \ \alpha &= \arctan\frac{Q}{P} \end{align*}

The maximum stress is located in cross section point which is furthest from the neutral axis.