notes/uni/mmme/1xxx/1026_maths_for_engineering/calculus.md

author, date, title, tags, uuid

author	date	title	tags	uuid
Alvie Rahman	\today	MMME1026 // Calculus	uni nottingham mechanical engineering mmme1026 maths calculus	126b21f8-e188-48f6-9151-5407f2b2b644

Calculus of One Variable Functions

Key Terms

Function

A function is a rule that assigns a unique value f(x) to each value x in a given domain.

The set of value taken by f(x) when x takes all possible value in the domain is the range of f(x).

Rational Functions

A function of the type

\frac{f(x)}{g(x)}

where f and g are polynomials, is called a rational function.

Its range has to exclude all those values of x where g(x) = 0.

Inverse Functions

Consider the function f(x) = y. If f is such that for each y in the range there is exactly one x in the domain, we can define the inverse f^{-1} as:

f^{-1}(y) = f^{-1}(f(x)) = x

Limits

Consider the following:

f(x) = \frac{\sin x}{x}

The value of the function can be easily calculated when x \neq 0, but when x=0, we get the expression \frac{\sin 0 }{0}. However, when we evaluate f(x) for values that approach 0, those values of f(x) approach 1.

This suggests defining the limit of a function

\lim_{x \rightarrow a} f(x)

to be the limiting value, if it exists, of f(x) as x gets approaches a.

Limits from Above and Below

Sometimes approaching 0 with small positive values of x gives you a different limit from approaching with small negative values of x.

The limit you get from approaching 0 with positive values is known as the limit from above:

\lim_{x \rightarrow a^+} f(x)

and with negative values is known as the limit from below:

\lim_{x \rightarrow a^-} f(x)

If the two limits are equal, we simply refer to the limit.

Important Functions

Exponential Functions

f(x) = e^x = \exp x

It can also be written as an infinite series:

\exp x = e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + ...

The two important limits to know are:

• as x \rightarrow + \infty, \exp x \rightarrow +\infty (e^x \rightarrow +\infty)
• as x \rightarrow -\infty, \exp x \rightarrow 0 (e^x \rightarrow 0)

Note that e^x > 0 for all real values of x.

Hyperbolic Functions (sinh and cosh)

The hyperbolic sine (\sinh) and hyperbolic cosine function (\cosh) are defined by:

\sinh x = \frac 1 2 (e^x - e^{-x}) \text{ and } \cosh x = \frac 1 2 (e^x + e^{-x}) \tanh = \frac{\sinh x}{\cosh x}

Some key facts about these functions:

• \cosh has even symmetry and \sinh and \tanh have odd symmetry
• as x \rightarrow + \infty, \cosh x \rightarrow +\infty and \sinh x \rightarrow +\infty
• \cosh^2x - \sinh^2x = 1
• $\tanh$'s limits are -1 and +1
• Derivatives:
  • \frac{\mathrm{d}}{\mathrm{d}x} \sinh x = \cosh x
  • \frac{\mathrm{d}}{\mathrm{d}x} \cosh x = \sinh x
  • \frac{\mathrm{d}}{\mathrm{d}x} \tanh x = \frac{1}{\cosh^2x}

Natural Logarithm

\ln{e^y} = \ln{\exp y} = y

Since the exponential of any real number is positive, the domain of \ln is x > 0.

Implicit Functions

An implicit function takes the form

f(x, y) = 0

To draw the curve of an implicit function you have to rewrite it in the form y = f(x). There may be more than one y value for each x value.

Differentiation

The derivative of the function f(x) is denoted by:

f'(x) \text{ or } \frac{\mathrm{d}}{\mathrm dx} f(x)

Geometrically, the derivative is the gradient of the curve y = f(x).

It is a measure of the rate of change of f(x) as x varies.

For example, velocity, v, is the rate of change of displacement, s, with respect to time, t, or:

v = \frac{\mathrm ds}{dt}

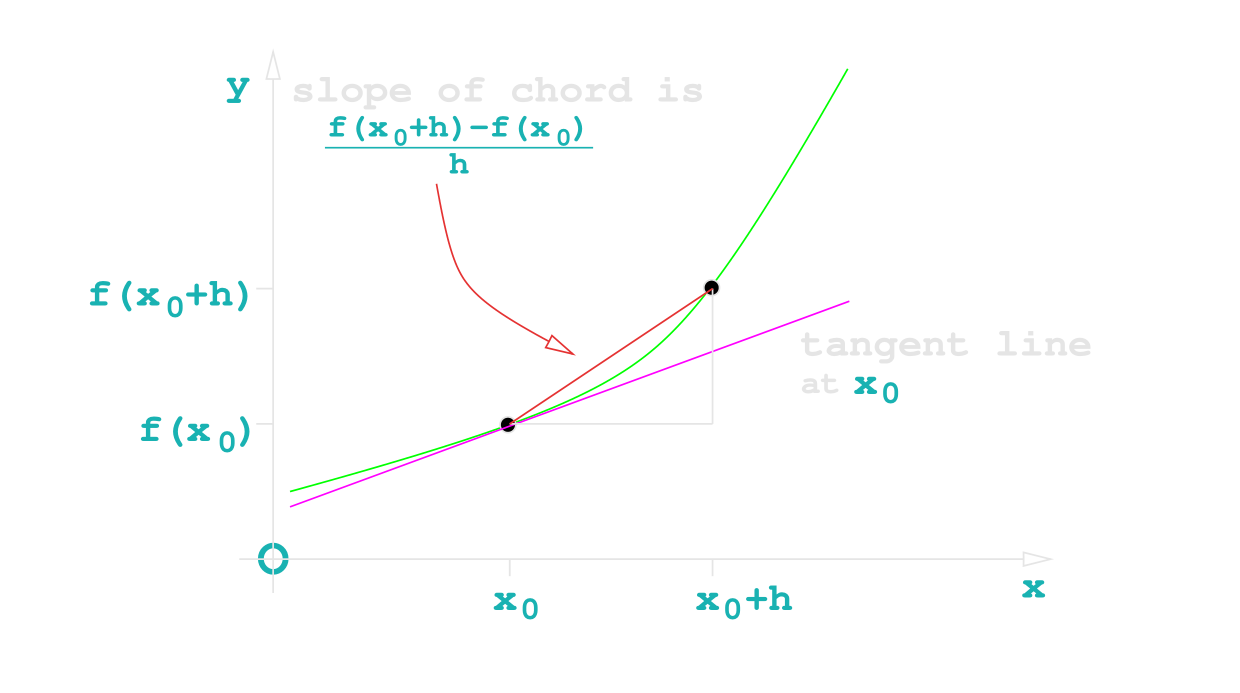
Formal Definition

As h\rightarrow 0, the clospe of the cord \rightarrow slope of the tangent, or:

f'(x_0) = \lim_{h\rightarrow0}\frac{f(x_0+h) - f(x_0)}{h}

whenever this limit exists.

Rules for Differentiation

Powers

\frac{\mathrm d}{\mathrm dx} x^n = nx^{-1}

Trigonometric Functions

\frac{\mathrm d}{\mathrm dx} \sin x = \cos x \frac{\mathrm d}{\mathrm dx} \cos x = \sin x

Exponential Functions

\frac{\mathrm d}{\mathrm dx} e^{kx} = ke^{kx} \frac{\mathrm d}{\mathrm dx} \ln kx^n = \frac n x

where n and k are constant.

Linearity

\frac{\mathrm d}{\mathrm dx} (f + g) = \frac{\mathrm d}{\mathrm dx} f + \frac{\mathrm d}{\mathrm dx} g

Product Rule

\frac{\mathrm d}{\mathrm dx} (fg) = \frac{\mathrm df}{\mathrm dx}g + \frac{\mathrm dg}{\mathrm dx}f

Quotient Rule

\frac{\mathrm d}{\mathrm dx} \frac f g = \frac 1 {g^2} \left( \frac{\mathrm df}{\mathrm dx} g - f \frac{\mathrm dg}{\mathrm dx} \right) \left( \frac f g \right)' = \frac 1 {g^2} (gf' - fg')

Chain Rule

Let

f(x) = F(u(x)) \frac{\mathrm df}{\mathrm dx} = \frac{\mathrm{d}F}{\mathrm du} \frac{\mathrm du}{\mathrm dx}

Example 1

Differentiate f(x) = \cos{x^2}.

Let u(x) = x^2, F(u) = \cos u

\frac{\mathrm df}{\mathrm dx} = -\sin u \cdot 2x = 2x\sin{x^2}

L'Hôpital's Rule

l'Hôpital's rule provides a systematic way of dealing with limits of functions like \frac{\sin x} x.

Suppose

\lim_{x\rightarrow{a}} f(x) = 0

and

\lim_{x\rightarrow{a}} g(x) = 0

and we want \lim_{x\rightarrow{a}} \frac{f(x)}{g(x)}.

If

\lim_{x\rightarrow{a}} \frac{f'(x)}{g'(x)} = L

where any L is any real number or \pm \infty, then

\lim_{x\rightarrow{a}} \frac{f(x)}{g(x)} = L

You can keep applying the rule until you get a sensible answer.

Graphs

Stationary Points

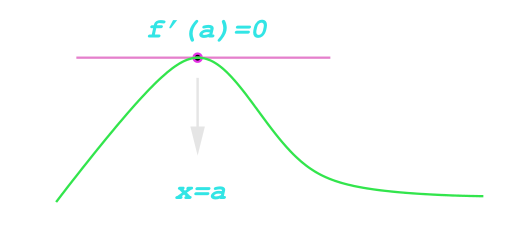
An important application of calculus is to find where a function is a maximum or minimum.

when these occur the gradient of the tangent to the curve, f'(x) = 0. The condition f'(x) = 0 alone however does not guarantee a minimum or maximum. It only means that point is a stationary point.

There are three main types of stationary points:

• maximum
• minimum
• point of inflection

Local Maximum

The point x = a is a local maximum if:

f'(a) = 0 \text{ and } f''(a) < 0

This is because f'(x) is a decreasing function of x near x=a.

Local Minimum

The point x = a is a local minimum if:

f'(a) = 0 \text{ and } f''(a) > 0

This is because f'(x) is a increasing function of x near x=a.

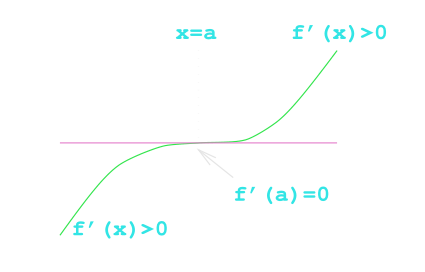
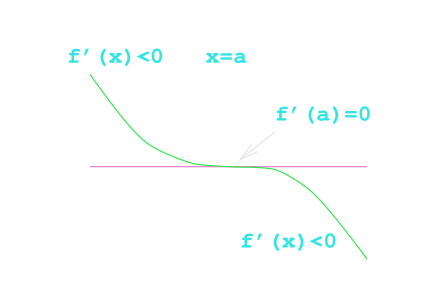
Point of Inflection

f'(a) = 0 \text{ and } f''(a) = 0 \text { and } f'''(a) \ne 0

f'''(a) > 0

f'''(a) < 0

Approximating with the Taylor series

The expansion

e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots

is an example of a Taylor series. These enable us to approximate a given function f(x) using a series which is often easier to calculate. Among other uses, they help us:

• calculate complicated function using simple arithmetic operations
• find useful analytical approximations which work for x near a given value (e.g. e^x \approx 1 + x for x near 0)
• Understand the behaviour of a function near a stationary point

Strategy

Suppose we know information about f(x) only at the point x=0. How can we find out about f for other values of x?

We could approximate the function by successive polynomials, each time matching more derivatives at x=0.

\begin{align*} g(x) = a_0 &\text{ using } f(0) \ g(x) = a_0 + a_1x &\text{ using } f(0), f'(0) \ g(x) = a_0 + a_1x + a_2x^2 &\text{ using } f(0), f'(0), f''(0) \ &\text{and so on...} \end{align*}

Example 1

For x near 0, approximate f(x) = \cos x by a quadratic.

1. Set f(0) = g(0:

   f(0) = 1 \rightarrow g(0) = a_0 = 1

2. Set f'(0) = g'(0:

   f'(0) = -\sin0 = 0 \rightarrow g'(0) = a_1 = 0

3. Set f''(0) = g''(0:

   f''(0) = -\cos = -1 \rightarrow g''(0) = 2a_2 = -1 \rightarrow a_2 = -0.5

So for x near 0,

\cos x \approx 1 - \frac 1 2 x^2

Check:

x	\cos x	1 - 0.5x^2
0.4	0.921061	0.920
0.2	0.960066	0.980
0.1	0.995004	0.995

General Case

Maclaurin Series

A Maclaurin series is a Taylor series expansion of a function about 0.

Any function f(x) can be written as an infinite Maclaurin Series

f(x) = a_0 + a_1x + a_2x^2 + a_3x^2 + \cdots

where

a_0 = f(0) \qquad a_n = \frac 1 {n!} \frac{\mathrm d^nf}{\mathrm dx^n} \bigg|_{x=0}

(|_{x=0} means evaluated at x=0)

Taylor Series

We may alternatively expand about any point x=a to give a Taylor series:

\begin{align*} f(x) = &f(a) + (x-a)f'(a) \ & + \frac 1 {2!}(x-a)^2f''(a) \ & + \frac 1 {3!}(x-a)^3f'''(a) \ & + \cdots + \frac 1 {n!}(x-a)^nf^{(n)}(a) \end{align*}

a generalisation of a Maclaurin series.

An alternative form of Taylor series is given by setting x = a+h where h is small:

f(a+h) = f(a) + hf'(a) + \cdots + \frac 1 {n!}h^nf^{(n)}(a) + \cdots

Taylor Series at a Stationary Point

If f(x) has a stationary point at x=a, then f'(a) = 0 and the Taylor series begins

f(x) = f(a) + \frac 1 2 f''(a)(x-a)^2 + \cdots

• If f''(a) > 0 then the quadratic part makes the function increase going away from x=a and we have a minimum
• If f''(a) < 0 then the quadratic part makes the function decrease going away from x=a and we have a maximum
• If f''(a) = 0 then we must include a higer order terms to determine what happens have a minimum

Integration

Integration is the reverse of differentiation.

Take velocity and displacement as an example:

\int\! v \mathrm dt = s + c

where c is the constant of integration, which is required for indefinite integrals.A

Definite Integrals

The definite integral of a function f(x) in the range a \le x \le b is denoted be:

\int^b_a \! f(x) \,\mathrm dx

If f(x) = F'(x) (f(x) is the derivative of F(x)) then

\int^b_a \! f(x) \,\mathrm dx = \left[F(x)\right]^b_a = F(b) - F(a)

Area and Integration

Approximate the area under a smooth curve using a large number of narrow rectangles.

Area under curve \approx \sum_{n} f(x_n)\Delta x_n.

As the rectangles get more numerous and narrow, the approximation approaches the real area.

The limiting value is denoted

\approx \sum_{n} f(x_n)\Delta x_n \rightarrow \int^b_a\! f(x) \mathrm dx

This explains the notation used for integrals.

Example 1

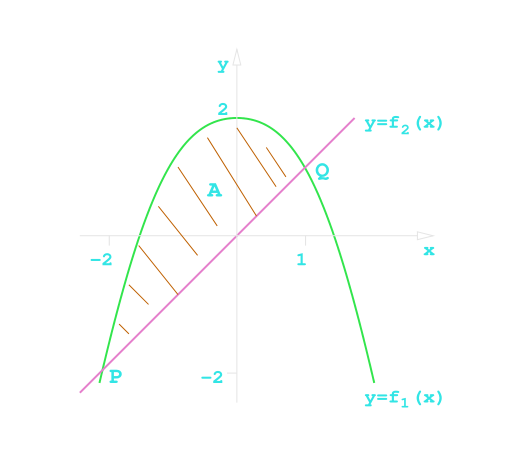
Calculate the area between these two curves:

\begin{align*} y &= f_1(x) = 2 - x^2 \ y &= f_2(x) = x \end{align*}

1. Find the crossing points P and Q

   \begin{align*} f_1(x) &= f_2(x) \ x &= 2-x^2 \ x &= 1 \ x &= -2 \end{align*}

2. Since f_1(x) \ge f_2(x) between P and Q

\begin{align*} A &= \int^1_{-2}! (f_1(x) - f_2(x)) \mathrm dx \ &= \int^1_{-2}! (2 - x^2 - x) \mathrm dx \ &= \left[ 2x - \frac 13 x^3 - \frac 12 x^2 \right]^1_{-2} \ &= \left(2 - \frac 13 - \frac 12 \right) - \left( -4 + \frac 83 - \frac 42 \right) \ &= \frac 92 \end{align*}

Techniques for Integration

Integration requires multiple techniques and methods to do correctly because it is a PITA.

These are best explained by examples so try to follow those rather than expect and explanation.

Integration by Substitution

Integration but substitution lets us integrate functions of functions.

Example 1

Find

I = \int\!(5x - 1)^3 \mathrm dx

1. Let w(x) = 5x - 1

2. \begin{align*} \frac{\mathrm d}{\mathrm dx} w &= 5 \ \frac 15 \mathrm dw &= \mathrm dx \end{align*}

3. The integral is then

   \begin{align*} I &= \int! w^3 \frac 15 \mathrm dw \ &= \frac 15 \cdot \frac 14 \cdot w^4 + c \ &= \frac{1}{20}w^4 + c \end{align*}

4. Finally substitute w out

I = \frac{(5x-1)^4}{20} + c

Example 2

Find

I = \int\! \cos x \sqrt{\sin x + 1} \mathrm dx

1. Let

   w(x) = \sin x + 1

2. Then

   \begin{align*} \frac{\mathrm d}{\mathrm dx} w = \cos x \ \mathrm dw = \cos x \mathrm dx \ \end{align*}

3. The integral is now

   \begin{align*} I &= \int! \sqrt w ,\mathrm dw \ &= \int! w^{\frac12} ,\mathrm dw \ &= \frac23w^{\frac32} + c \end{align*}

4. Finally substitute w out to get:

   I = \frac23 (\sin x + 1)^{\frac32} + c

Example 3

Find

I = \int^{\frac\pi2}_0\! \cos x \sqrt{\sin x + 1} \,\mathrm dx

1. Use the previous example to get to

   I = \int^2_1\! \sqrt w \,\mathrm dw = \frac23w^{\frac32} + c

2. Since w(x) = \sin x + 1 the limits are:

   \begin{align*} x = 0 &\rightarrow w = 1\ x = \frac\pi2 &\rightarrow w = 2 \end{align*}

3. This gives us

   I = \left[ \frac23w^{\frac32} \right]^2_1 = \frac23 (2^{\frac23} = 1)

Example 4

Find

I = \int^1_0\! \sqrt{1 - x^2} \,\mathrm dx

1. Try a trigonmetrical substitution:

\begin{align*} x &= \sin w \ \ \frac{\mathrm dx}{\mathrm dw} = \cos w \ \mathrm dx = \cos 2 ,\mathrm dw \ \end{align*}

\begin{align*} x=0 &\rightarrow w=0 \ x=1 &\rightarrow w=\frac\pi2 \end{align*}

3. Therefore

   \begin{align*} I &= \int^{\frac\pi2}_0! \sqrt{1 - \sin^2 w} \cos w ,\mathrm dw \ &= \int^{\frac\pi2}_0! \cos^w w ,\mathrm dw \end{align*}

   But \cos(2w) = 2\cos^2w - 1 so:

   \cos^2w = \frac12 \cos(2w) + \frac12

   Hence

   \begin{align*} I &= \int^{\frac\pi2}_0! \frac12 \cos(2w) + \frac12 ,\mathrm dw \ &= \left[ \frac14 \sin(2w) + \frac w2 \right]^{\frac\pi2}_0 \ &= \left( \frac14 \sin\pi + \frac\pi4 \right) - 0 \ &= \frac\pi4 \end{align*}

Integration by Parts

uv = \int\! u\frac{\mathrm dv}{\mathrm dx} \,\mathrm dx + \int\! \frac{\mathrm du}{\mathrm dx}v \,\mathrm dx

or

\int\! u\frac{\mathrm dv}{\mathrm dx} \,\mathrm dx = uv - \int\! \frac{\mathrm du}{\mathrm dx}v \,\mathrm dx

This technique is derived from integrating the product rule.

Example 1

Find

I = \int\! \ln x \,\mathrm dx

1. Use

   \int\! u\frac{\mathrm dv}{\mathrm dx} \,\mathrm dx = uv - \int\! \frac{\mathrm du}{\mathrm dx}v \,\mathrm dx

2. Set u = \ln x
   and v' = 1.

3. This means that u' = \frac1x and v = x.

\begin{align*} I &= x\ln x - \int! x\cdot\frac1x ,\mathrm dx + c \ &= x\ln x - \int! ,\mathrm dx + c \ &= x\ln x - x + c \ \end{align*}

Application of Integration

Differential Equations

Consider the equation

\frac{\mathrm dy}{\mathrm dx} = y^2

To find y, is not a straightforward integration:

y = \int\!y^2 \,\mathrm dx

The equation above does not solve for y as we can't integrate the right until we know y... which is what we're trying to find.

This is an example of a first order differential equation. The general form is:

\frac{\mathrm dy}{\mathrm dx} = F(x, y)

Separable Differential Equations

A first order diferential equation is called separable if it is of the form

\frac{\mathrm dy}{\mathrm dx} = f(x)g(y)

We can solve these by rearranging:

\frac1{g(y} \cdot \frac{\mathrm dy}{\mathrm dx} = f(x) \int\! \frac1{g(y)} \,\mathrm dy = \int\! f(x) \,\mathrm dx + c

Example 1

Find y such that

\frac{\mathrm dy}{\mathrm dx} = ky

where k is a constant.

Rearrange to get

\begin{align*} \int! \frac1y ,\mathrm dy &= \int! k \mathrm dx + c \ \ln y &= kx + c \ y &= e^{kx + c} = e^ce^{kx} \ &= Ae^{kx} \end{align*}

where A = e^c is an arbitrary constant.