notes/mechanical/mmme1048_fluid_mechanics.md

author	date	title	tags
Alvie Rahman	\today	MMME1048 // Fluid Mechanics	uni nottingham mechanical engineering fluid_mechanics mmme1048

Lecture 1 // Properties of Fluids (2021-10-06)

What is a Fluid?

• A fluid may be liquid, vapor, or gas
• No permanent shape
• Consists of atoms in random motion and continual collision
• Easy to deform
• Liquids have fixed volume, gasses fill up container
• A fluid is a substance for wich a shear stress tends to produce unlimited, continuous deformation

Shear Forces

• For a solid, application of shear stress causes a deformation which, if not too great (elastic), is not permanent and solid regains original positon
• For a fluid, continuious deformation takes place as the molecules slide over each other until the force is removed
• A fluid is a substance for wich a shear stress tends to produce unlimited, continuous deformation

Density

• Density: \rho = \frac m V
• Specific Density: v = \frac 1 \rho

Obtaining Density

• Find mass of a given volume or volume of a given mass

• This gives average density and assumes density is the same throughout

  • This is not always the case (like in chocolate chip ice cream)
  • Bulk density is often used to refer to average density

Engineering Density

• Matter is not continuous on molecular scale
• For fluids in constant motion, we take a time average
• For most practical purposes, matter is considered to be homogenous and time averaged

Pressure

• Pressure is a scalar quantity

• Gases cannot sustain tensile stress, liquids a negligible amount

• There is a certain amount of energy associated with the random continuous motion of the molecules

• Higher pressure fluids tend to have more energy in their molecules

How Does Molecular Motion Create Force?

• When molecules interact with each other, there is no net force

• When they interact with walls, there is a resultant force perpendicular to the surface

• Pressure caused my molecule: p = \frac {\delta{}F}{\delta{}A}

• If we want total force, we have to add them all up

• F = \int \mathrm{d}F = \int p\, \mathrm{d}A
  • If pressure is constant, then this integrates to F = pA
  • These equations can be used if pressure is constant of average value is appropriate
  • For many cases in fluids pressure is not constant

Pressure Variation in a Static Fluid

• A fluid at rest has constant pressure horizontally
• That's why liquid surfaces are flat
• But fluids at rest do have a vertical gradient, where lower parts have higher presure

How Does Pressure Vary with Depth?

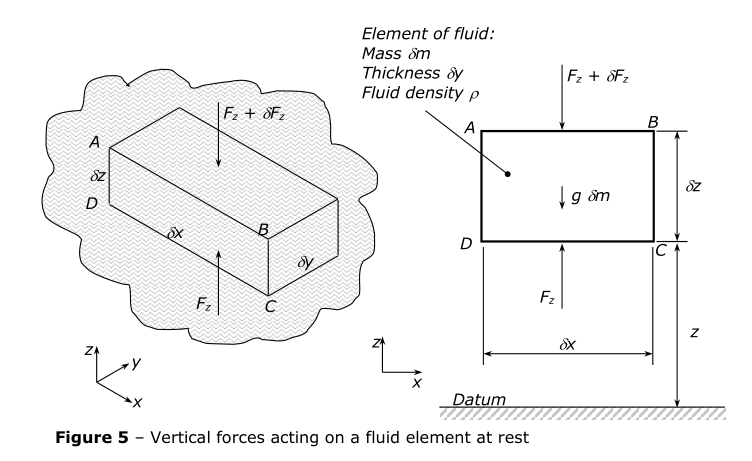
Let fluid pressure be p at height z, and p + \delta p at z + \delta z.

Force F_z acts upwards to support the fluid, countering pressure p.

Force $F_z + \delta F_z$acts downwards to counter pressure p + \delta p and comes from the weight of the liquid above.

Now:

\begin{align*} F_z &= p\delta x\delta y \ F_z + \delta F_z &= (p + \delta p) \delta x \delta y \ \therefore \delta F_z &= \delta p(\delta x\delta y) \end{align*}

Resolving forces in z direction:

\begin{align*} F_z - (F_z + \delta F_z) - g\delta m &= 0 \ \text{but } \delta m &= \rho\delta x\delta y\delta z \ \therefore -\delta p(\delta x\delta y) &= g\rho(\delta x\delta y\delta z) \ \text{or } \frac{\delta p}{\delta z} &= -\rho g \ \text{as } \delta z \rightarrow 0,, \frac{\delta p}{\delta z} &\rightarrow \frac{dp}{dz}\ \therefore \frac{dp}{dz} &= -\rho g\ \Delta p &= \rho g\Delta z \end{align*}

The equation applies for any fluid. The -ve sign indicates that as z, height, increases, p, pressure, decreases.

Absolute and Gauge Pressure

• Absolute Pressure is measured relative to zero (a vacuum)

• Guage pressure = absolute pressure - atmospheric pressure

  • Often used in industry

• If abs. pressure = 3 bar and atmospheric pressure is 1 bar, then gauge pressure = 2 bar

• Atmospheric pressure changes with altitude

Compressibility

• All fluids are compressible, especially gasses
• Most liquids can be considered incompressible most of the time (and will be in MMME1048, but may not be in future modules)

Surface Tension

• In a liquid, molecules are held together by molecular attraction
• At a boundry between two fluids this creates "surface tension"
• Surface tension usually has the symbol \gamma

Ideal Gas

• No real gas is perfect, although many are similar

• We define a specific gas constant to allow us to analyse the behaviour of a specific gas:

  R = \frac {\tilde R}{\tilde m}

  (Universal Gas Constant / molar mass of gas)

• Perfect gas law

  pV=mRT

  or

  p = \rho RT
  • Pressure always in Pa
  • Temperature always in K

Units and Dimentional Analysis

• It is usually better to use SI units
• If in doubt, DA can be useful to check that your answer makes sense

Lecture 2 // Manometers (2021-10-13)

p_{1,gauge} = \rho g(z_2-z_1)

• Manometers work on the principle that pressure along any horizontal plane through a continuous fluid is constant
• Manometers can be used to measure the pressure of a gas, vapour, or liquid
• Manometers can measure higher pressures than a piezometer
• Manometer fluid and working should be immiscible (don't mix)

\begin{align*} p_A &= p_{A'} \ p_{bottom} &= p_{top} + \rho gh \ \rho_1 &= density,of,fluid,1 \ \rho_2 &= density,of,fluid,2 \end{align*}

Left hand side:

p_A = p_1 + \rho_1g\Delta z_1

Right hand side:

p_{A'} = p_{at} + \rho_2g\Delta z_2

Equate and rearrange:

\begin{align*} p_1 + \rho_1g\Delta z_1 &= p_{at} + \rho_2g\Delta z_2 \ p_1-p_{at} &= g(\rho_2\Delta z_2 - \rho_1\Delta z_1) \ p_{1,gauge} &= g(\rho_2\Delta z_2 - \rho_1\Delta z_1) \end{align*}

If \rho_a << \rho_2:

\rho_{1,gauge} \approx \rho_2g\Delta z_2

Differential U-Tube Manometer

• Used to find the difference between two unknown pressures
• Can be used for any fluid that doesn't react with manometer fluid
• Same principle used in analysis

\begin{align*} p_A &= p_{A'} \ p_{bottom} &= p_{top} + \rho gh \ \rho_1 &= density,of,fluid,1 \ \rho_2 &= density,of,fluid,2 \end{align*}

Left hand side:

p_A = p_1 + \rho_wg(z_C-z_A)

Right hand side:

p_B = p_2 + \rho_wg(z_C-z_B)

Right hand manometer fluid:

p_{A'} = p_B + \rho_mg(z_B - z_a)

\begin{align*} p_{A'} &= p_2 + \rho_mg(z_C - z_B) + \rho_mg(z_B - zA)\ &= p_2 + \rho_mg(z_C - z_B) + \rho_mg\Delta z \ \ p_A &= p_{A'} \ p_1 + \rho_wg(z_C-z_A) &= p_2 + \rho_mg(z_C - z_B) + \rho_mg\Delta z \ p_1 - p_2 &= \rho_wg(z_C-z_B-z_C+z_A) + \rho_mg\Delta z \ &= \rho_wg(z_A-z_B) + \rho_mg\Delta z \ &= -\rho_wg\Delta z + \rho_mg\Delta z \end{align*}

Angled Differential Manometer

• If the pipe is sloped then

  p_1-p_2 = (\rho_m-\rho_w)g\Delta z + \rho_wg(z_{C2} - z_{C1})

• p_1 > p_2 as p_1 is lower

• If there is no flow along the tube, then

  p_1 = p_2 + \rho_wg(z_{C2} - z_{C1})