notes/uni/mmme/2051_electromechanical_devices/digital_electronics.md

author	date	title	tags	uuid	lecture_slides	lecture_notes	exercise_sheets
Akbar Rahman	\today	MMME2051 // Digital Electronics	digital serial parallel encoders shaft_encoders	7d355a2f-68c7-4352-a164-7d51006ca137	./lecture_slides/MMME2051EMD_Lecture4.pdf ./lecture_slides/MMME2051EMD_Lecture5.pdf		./exercise_sheets/Exercise Sheet 6 - Digital Electonics 1.pdf ./exercise_sheets/Exercise Sheet 7 - Digital Electonics 2.pdf

Errata

Lecture Slides 5, p56

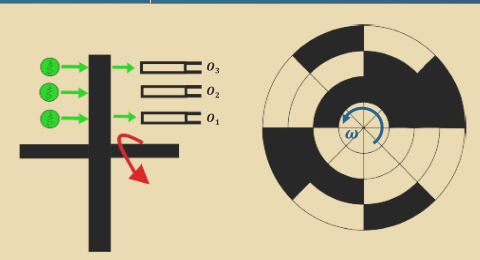
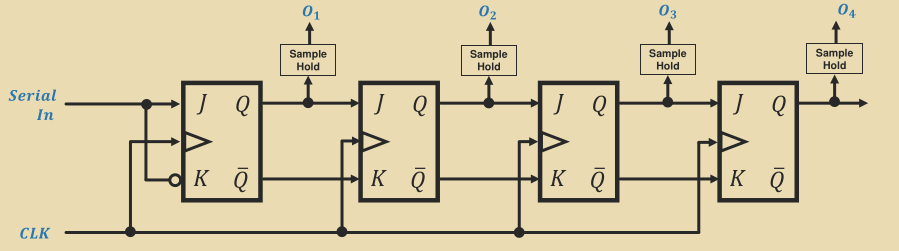
1. The graph showing values of O_1, O_2, and O_3 are incorrect:

• O_3 should stay low throughout
• O_2 should stay low until after the fourth pulse
• O_1 should be low until the third pulse, high between third and fourth, and then go back to low

2. There is no mention that O_4 is the most significant bit and O_1 the least.

Lecture Slides 5, p62-91

1. The title should be Digital-to-Analog Converter (DAC)

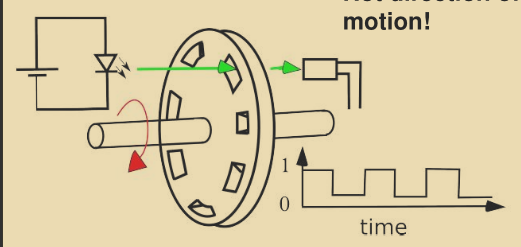
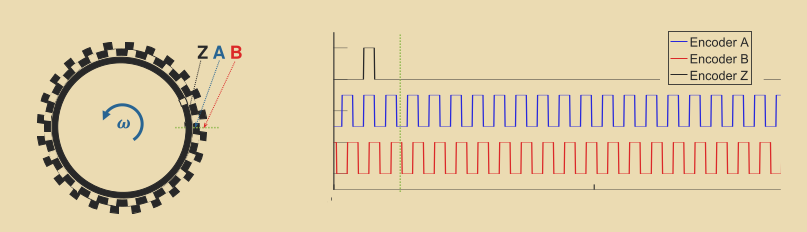
Shaft Encoder

A shaft encoder can provide angular position, angular speed, and direction.

Memory in Computers

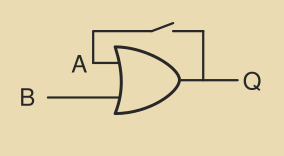
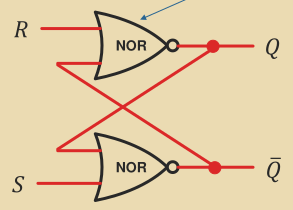
An OR gate can be used to create a latch which will stay high until it is reset:

Set/Reset Latch

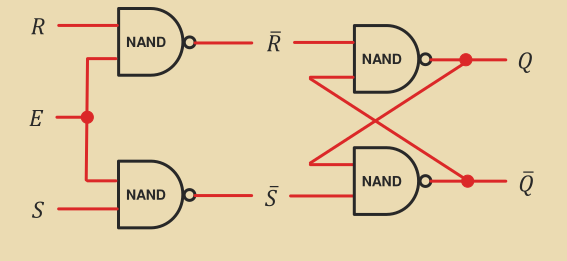
An equivalent circuit can be built by replacing the NOR gates with NAND gates and taking NOTing the inputs before applying them (lecture 5 slides, p27).

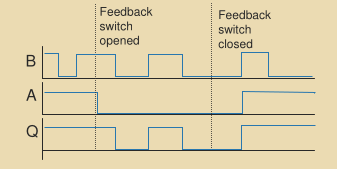
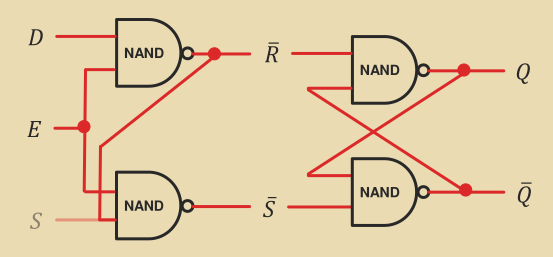
Enabling a Latch

Delay Gated Latch

This latch allows memory to be set/reset without having a reset line.

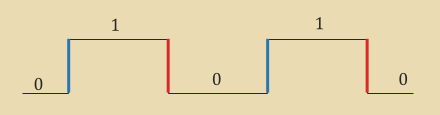
Clock

A clock signal is a square waveform. The higher the frequency of the signal, the faster processing can happen. One step of processing is expected to happen per clock pulse. A clock pulse is usually considered to be its rising edge:

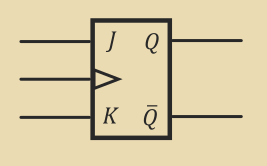
JK Flip-Flop

Flip-flops differ from latches mainly by the fact they are edge triggered (triggered by the edge of the clock pulse, rather than by change in input signals).

Q_\text{next} = J \bar Q + \bar K Q

Clock	J	K	Q_\text{next}	\bar Q_\text{next}
0 \rightarrow 1	0	0	Q	\bar Q
0 \rightarrow 1	0	1	0	1
0 \rightarrow 1	1	0	1	0
0 \rightarrow 1	1	1	\bar Q	Q

Serial to Parallel Conversion with JK Flip-Flops

There are errors in lecture slides relating to this section.

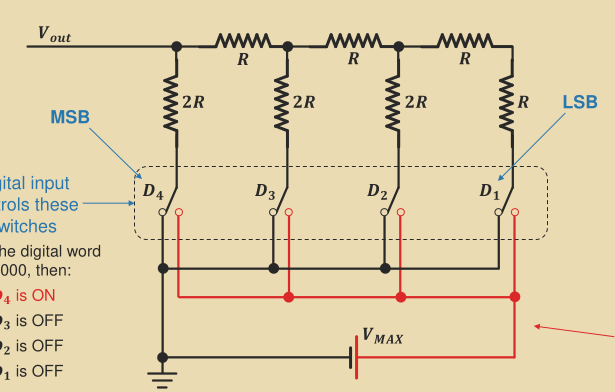
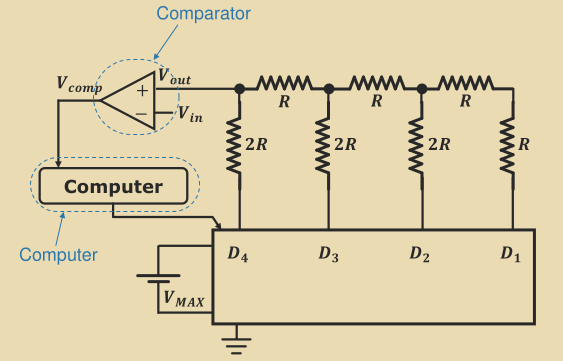
Digital to Analog Converter (DAC)

V_\text{out} can be expressed as the following:

V_\text{out} = \sum D_n\frac{1}{2^n}V_\text{max}

where D_n is 1 for an high input and 0 for a low input.

The lecture slides go through the circuitry step by step (lecture 5, p62-91).

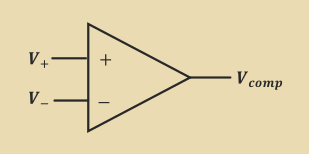
Comparator

If the positive input is larger than the negative, the output is high.

Analog Digital Converter (ADC)

Explanation in lecture slides (lecture 5, p93-94) and on flash converters (lecture 5, p95).