notes/uni/mmme/2044_design_manufacture_and_project/shaft_design.md

author	date	title	tags	uuid
Akbar Rahman	\today	MMME2044 // Shaft Design	mmme2044 shafts uni	8e0928a6-c20c-4f80-9691-beb2defa4022

Shaft Design Considerations

• Function and loading
• Size and connection to components
• Material selection and treatments
• Deflection and rigidity
• Stress and strength
• Critical speed
• Manufacturing constraints

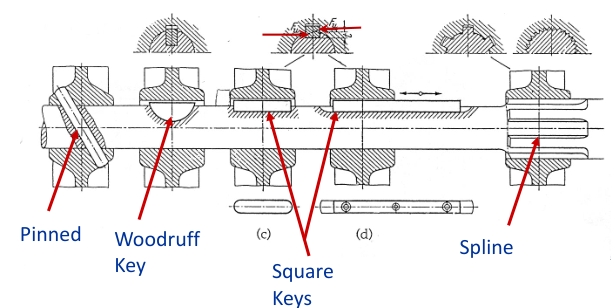
Shaft-Hub Connections

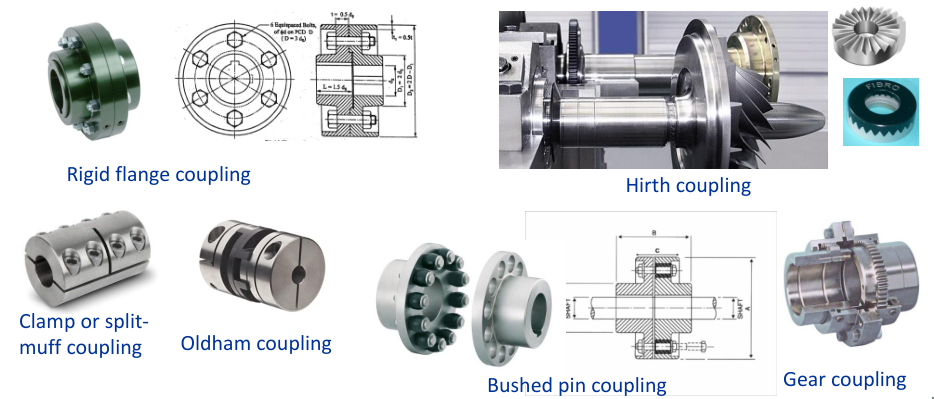
Shaft-Shaft Connections

Shaft-shaft connections can use either rigid or flexible couplings.

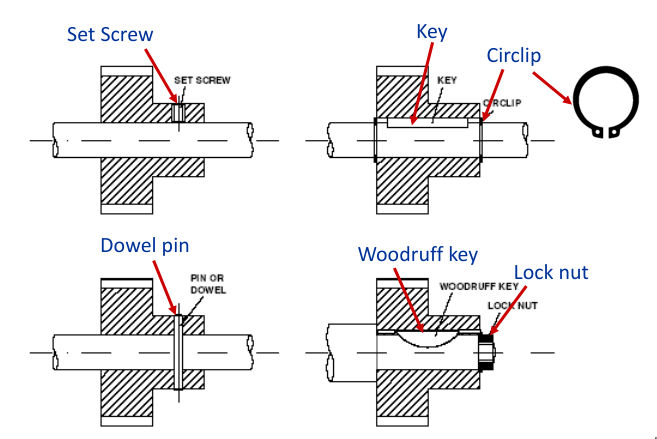
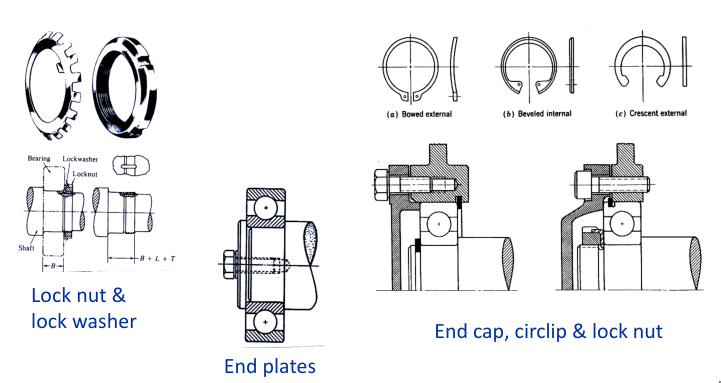
Location of Bearing on Shaft

Shaft Loading

• Axial stresses

  • cause by self-weight in vertical shafts
  • due to axial restraint at bearings and associated axial load

• bending stress

  • due to bending moment in belt drivers, gear forces, mounted component weights
  • dynamic forces which can load to fatigue and resonance

• shear stresses

  • due to torque load/direct shear

Shaft Diameter (ASME Design Code)

d = \left[
        \frac{32n_s}{\pi}
        \sqrt{
                \left(\frac{M}{\sigma_e}\right)^2 
                + \frac34 \left(\frac{T}{\sigma_y}\right)^2
        }
      \right]^{\frac13}

where:

• n_s is safety factor
• M is max bending moment (Nm)
• T is max torque (Nm)
• \sigma_e is endurance limit stress (Pa)
• \sigma_y is yield strength of shaft (Pa)

ASME Design Code Derivation

• Bending moment creates alternating tensile/compressive stresses (\sigma_a):

  \begin{align} \sigma &= \frac{My}{I} \ I &= \frac{\pi d^4}{64} \end{align}

  Combine to get:

  \sigma_a = \frac{32M}{\pi d^3}

• Torque normally generates constant shear stress (\tau_m):

  \begin{align} \tau &= \frac{TR}{J} \ J &= \frac{\pi d^4}{32} \end{align}

  Combine to get:

  \rightarrow \tau_m = \frac{16T}{\pi d^3}

• von Mises stress in plane stress condition:

  \sigma_\text{von Mises} = (\sigma^2 + 3\tau^2)^{\frac12}

• ASME Fatigue Failure Criterion

  \left(\frac{n_s\sigma_a}{\sigma_e}\right)^2 + \left(\frac{n_s\sigma_m}{\sigma_Y}\right)^2 = 1

  Finally substitute \sigma_a and \tau_m to make d the subject.

Endurance Limit Stress, \sigma_e

\sigma_e is the level of stress with which fatigue failure wouldn't occur in cycling or alternating load conditions:

• \sigma at failure decreases with the number of cycles up until a certain point (\sigma_e after around 10^6 cycles)
• if you never exceed this point then the material will last for "infinite" cycles
• most steels have this fatigue behaviour so they are often used for shafts

Time for a silly equation:

\sigma_e = k_ak_bk_ck_dk_ek_fk_g\sigma_e'

where:

• k_a --- surface factor
• k_b --- size factor
• k_c --- reliability factor
• k_d --- temperature factor
• k_e --- duty cycle factor
• k_f --- fatigue stress concentration factor
• k_g --- miscellaneous effects factor
• \sigma_e' --- endurance limit of test specimen

this is a joke of an equation

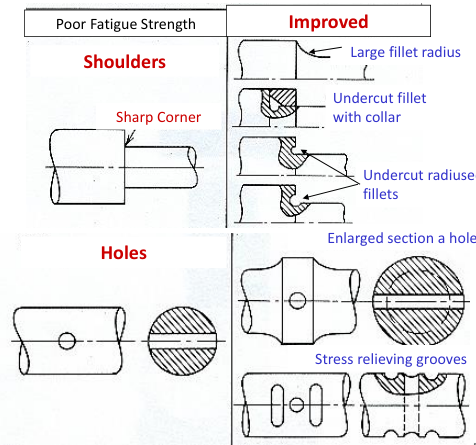
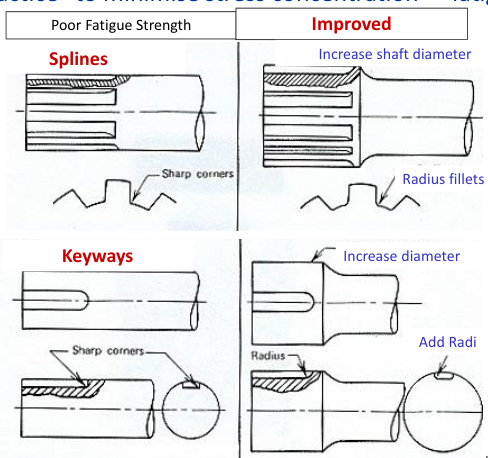
Reducing Stress Concentrations

Critical Speed of Shaft (Natural Frequency)

• operational speed of shat should be half the critical speed

• Centre of Mass should be on the Centre of Rotation

• in practice this is not the case

• this imbalance causes a deflection (due to centrifugal force, mr\omega^2

• the critical speed (or natural frequency) is the speed at which the shaft is unstable

  when this is the case it may cause damage to the shaft, bearings, and other destructive vibrations

Critical Speed Equation

\omega_c = \sqrt\frac{g}{\delta_\text{st}}

where g is acceleration due to gravity and \delta_\text{st} is static deflection of the shaft.

Rayleigh Ritz Equation

When you have multiple masses the Rayleigh-Ritz equation may be more suitable:

\omega_c = \sqrt{g\frac{\Sigma w_i\delta_i}{\Sigma w_i\delta_i^2}} 

where w_i is the weight of node i and \delta_i is the static deflection at node i.

Shaft Deflection

• Shaft deflection is required to determine the critical speed.

• Macaulay's method for the deflection in beam bending:

  \frac{\mathrm{d}^2y}{\mathrm{d}x^2} = \frac{M}{EI}

  y = \int^x_0\int^x_0\left(\frac{M}{EI}\right) \mathrm{d}x + C_1x + C_2

Shaft Deflection Equations

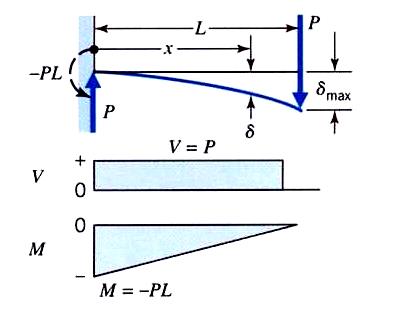
• Maximum deflection:

  \delta_\text{max} = \frac{PL^3}{3EI}

• Deflection at any point x

  \delta = \frac{Px^3}{6EI}(3L-x)

• Maximum deflection:

  \delta_\text{max} = \frac{PL^3}{48EI}

• Deflection at any point:

  \delta = \frac{Px}{12EI} \left(\frac{3L^2}{4} - x^2 \right)

• Maximum deflection

  \delta_\text{max} = \frac{Pb^2L}{3EI}

• Deflection at any point

  • For 0 \le x \le a:

    \delta = \frac{Pbx}{6aEI}(x^2-a^2)

  • For 0 \le z \le b:

    \delta = \frac{Pbx}{6aEI}\left(z^3 - b(2L+b) + 2b^2L\right)

Safety Factor

Safety Factor (also known as reserve factor) is a simple way to accommodate for uncertainties in design.

Simply multiply the maximum stresses and loads you expect by the safety factor, n_s, and assume that as your maximum stress and load.

n_s	Operational conditions and use of materials
1.25-1.50	Reliable materials under controlled conditions, known stresses with certainty
1.50-2.00	Well-known materials under reasonably constant environmental condition, known stresses
2.00-2.50	Average materials subjected to known loads and stresses and environment (LSE)
2.50-3.00	Lesser well-known materials under average conditions LSE
3.00-3.40	Untried materials under average conditions of stresses and environment, or well known materials under uncertain LSE