notes/mechanical/mmme1028_statistics_and_dynamics.md

author	date	tags	title
Alvie Rahman	\today	uni nottingham mmme1028 maths statics dynamics	MMME1028 // Statics and Dynamics

Lecture L1.1, L1.2

Lecture L1.1 Exercises

Can be found here.

Lecture L1.2 Exercises

Can be found here here

Newton's Laws

1. Remains at constant velocity unless acted on by external force

2. Sum of forces on body is equal to mass of body multiplied by acceleration

   1st Law is a special case of 2nd

3. When one body exerts a force on another, 2nd body exerts force simultaneously of equal magnitude and opposite direction

Equilibrium

• Body is in equilibrium if sum of all forces and moments acting on body are 0

Example

Determine force F and x so that the body is in equilibrium.

1. Check horizontal equilibrium

   \sum{F_x} = 0

2. Check vertical equilibrium

   \sum{F_y} = 8 - 8 + F = 0

   F = 2

3. Take moments about any point

   \sum{M(A)} = 8\times{}2 - F(2+x) = 0

   F(2+x) = 16)

   x = 6

Free Body Diagrams

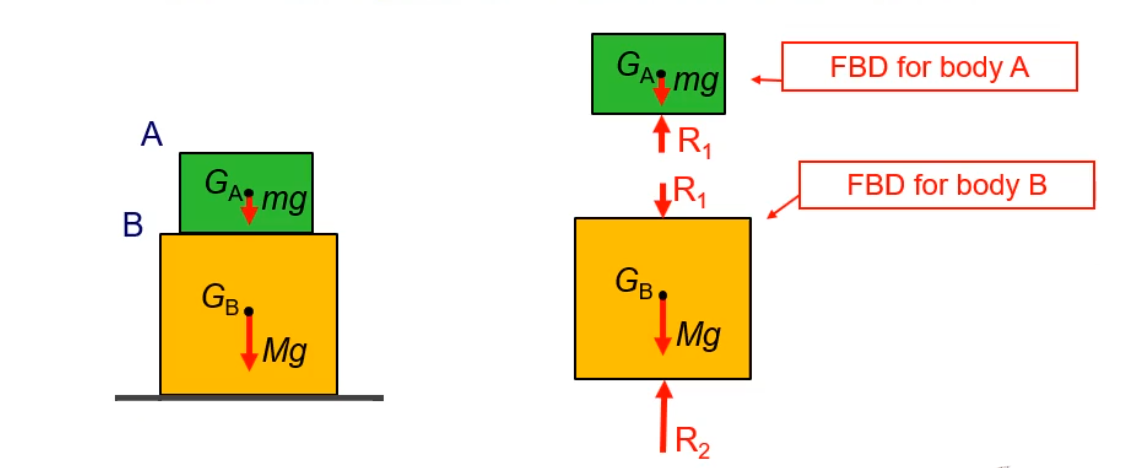
A free body diagram is a diagram of a single (free) body which shows all the external forces acting on the body.

Where there are several bodies or subcomponents interacting as a complex system, each body is drawn separately:

Friction

• Arises between rough surfaces and always acts at right angles to the normal reaction force (R) in the direction to resist motion.
• The maximum value of friction F is F_{max} = \mu{}R, where \mu{} is the friction coefficient
• F_{max} is also known as the point of slip

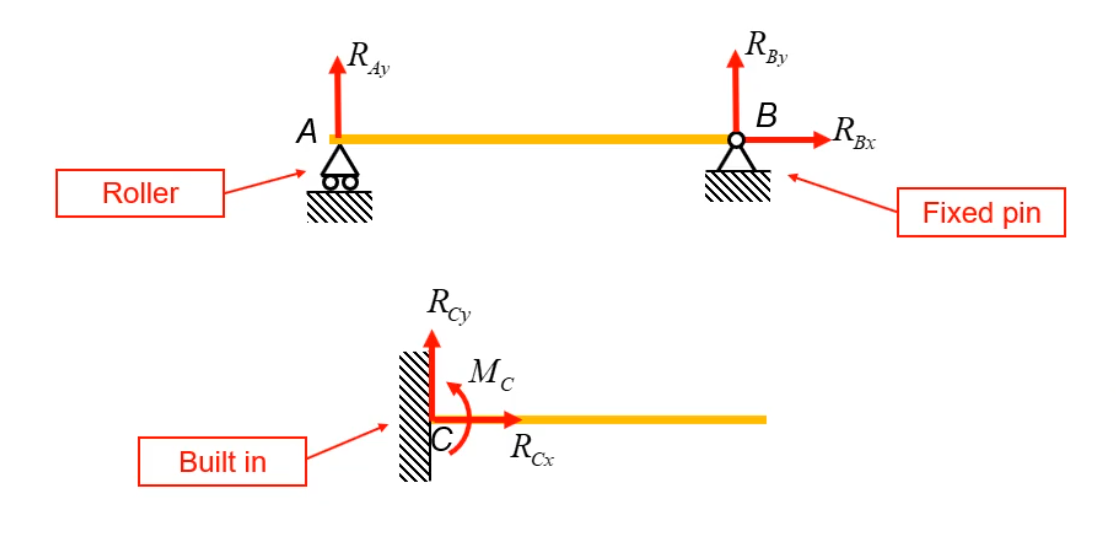
Reactions at Supports

There are three kinds of supports frequently encountered in engineering problems:

Principle of Force Transmissibility

A force can be move dalong line of action without affecting equilibrium of the body which it acts on:

This principle can be useful in determining moments.

Two-Force Bodies

• If a body has only 2 forces, then the forces must be collinear, equal, and opposite:

  

  The forces must be collinear so a moment is not created

Three-Force Bodies

• If a body in equilibrium has only three forces acting on it, then the lines of actions must go through one point:

  

  This is also to not create a moment

• The forces must form a closed triangle (\sum{F} = 0)

Naming Conventions

Term	Meaning
light	no mass
heavy	body has mass
smooth	there is no friction
rough	contact has friction
at the point of slip	one tangential reaction is F_{max}
roller	a support only creating normal reaction
rigid pin	a support only providing normal and tangential reactions
built-in	a support proviting two reaction components and a moment

Tips to Solve (Difficult) Problems

1. Make good quality clear and big sketches
2. Label all forces, dimensions, relevant points
3. Explain and show your thought process---write complete equations
4. Follow standard conventions in equations and sketches
5. Solve everything symbolically (algebraicly) until the end
6. Check your answers make sense
7. Don't forget the units