notes/mechanical/mmme1048_fluid_mechanics.md

author	date	title	tags
Alvie Rahman	\today	MMME1048 // Fluid Mechanics Intro and Statics	uni nottingham mechanical engineering fluid_mechanics mmme1048 fluid_statics

Properties of Fluids

What is a Fluid?

• A fluid may be liquid, vapor, or gas
• No permanent shape
• Consists of atoms in random motion and continual collision
• Easy to deform
• Liquids have fixed volume, gasses fill up container
• A fluid is a substance for wich a shear stress tends to produce unlimited, continuous deformation

Shear Forces

• For a solid, application of shear stress causes a deformation which, if not too great (elastic), is not permanent and solid regains original positon
• For a fluid, continuious deformation takes place as the molecules slide over each other until the force is removed
• A fluid is a substance for wich a shear stress tends to produce unlimited, continuous deformation

Density

• Density: \rho = \frac m V
• Specific Density: v = \frac 1 \rho

Obtaining Density

• Find mass of a given volume or volume of a given mass

• This gives average density and assumes density is the same throughout

  • This is not always the case (like in chocolate chip ice cream)
  • Bulk density is often used to refer to average density

Engineering Density

• Matter is not continuous on molecular scale
• For fluids in constant motion, we take a time average
• For most practical purposes, matter is considered to be homogenous and time averaged

Pressure

• Pressure is a scalar quantity

• Gases cannot sustain tensile stress, liquids a negligible amount

• There is a certain amount of energy associated with the random continuous motion of the molecules

• Higher pressure fluids tend to have more energy in their molecules

How Does Molecular Motion Create Force?

• When molecules interact with each other, there is no net force

• When they interact with walls, there is a resultant force perpendicular to the surface

• Pressure caused my molecule: p = \frac {\delta{}F}{\delta{}A}

• If we want total force, we have to add them all up

•  F = \int \mathrm{d}F = \int p\, \mathrm{d}A 

  • If pressure is constant, then this integrates to F = pA
  • These equations can be used if pressure is constant of average value is appropriate
  • For many cases in fluids pressure is not constant

Pressure Variation in a Static Fluid

• A fluid at rest has constant pressure horizontally
• That's why liquid surfaces are flat
• But fluids at rest do have a vertical gradient, where lower parts have higher presure

How Does Pressure Vary with Depth?

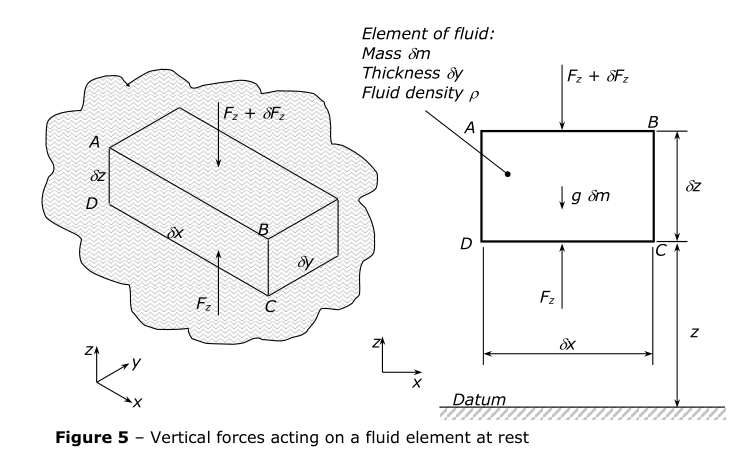
Let fluid pressure be p at height z, and p + \delta p at z + \delta z.

Force F_z acts upwards to support the fluid, countering pressure p.

Force $F_z + \delta F_z$acts downwards to counter pressure p + \delta p and comes from the weight of the liquid above.

Now:

\begin{align*} F_z &= p\delta x\delta y \ F_z + \delta F_z &= (p + \delta p) \delta x \delta y \ \therefore \delta F_z &= \delta p(\delta x\delta y) \end{align*}

Resolving forces in z direction:

\begin{align*} F_z - (F_z + \delta F_z) - g\delta m &= 0 \ \text{but } \delta m &= \rho\delta x\delta y\delta z \ \therefore -\delta p(\delta x\delta y) &= g\rho(\delta x\delta y\delta z) \ \text{or } \frac{\delta p}{\delta z} &= -\rho g \ \text{as } \delta z \rightarrow 0,, \frac{\delta p}{\delta z} &\rightarrow \frac{dp}{dz}\ \therefore \frac{dp}{dz} &= -\rho g\ \Delta p &= \rho g\Delta z \end{align*}

The equation applies for any fluid. The -ve sign indicates that as z, height, increases, p, pressure, decreases.

Absolute and Gauge Pressure

• Absolute Pressure is measured relative to zero (a vacuum)

• Guage pressure = absolute pressure - atmospheric pressure

  • Often used in industry

• If abs. pressure = 3 bar and atmospheric pressure is 1 bar, then gauge pressure = 2 bar

• Atmospheric pressure changes with altitude

Compressibility

• All fluids are compressible, especially gasses
• Most liquids can be considered incompressible most of the time (and will be in MMME1048, but may not be in future modules)

Surface Tension

• In a liquid, molecules are held together by molecular attraction
• At a boundry between two fluids this creates "surface tension"
• Surface tension usually has the symbol $$\gamma$$

Ideal Gas

• No real gas is perfect, although many are similar

• We define a specific gas constant to allow us to analyse the behaviour of a specific gas:

   R = \frac {\tilde R}{\tilde m} 

  (Universal Gas Constant / molar mass of gas)

• Perfect gas law

  pV=mRT

  or

   p = \rho RT

  • Pressure always in Pa
  • Temperature always in K

Units and Dimentional Analysis

• It is usually better to use SI units
• If in doubt, DA can be useful to check that your answer makes sense

Fluid Statics

Manometers

p_{1,gauge} = \rho g(z_2-z_1)

• Manometers work on the principle that pressure along any horizontal plane through a continuous fluid is constant
• Manometers can be used to measure the pressure of a gas, vapour, or liquid
• Manometers can measure higher pressures than a piezometer
• Manometer fluid and working should be immiscible (don't mix)

\begin{align*} p_A &= p_{A'} \ p_{bottom} &= p_{top} + \rho gh \ \rho_1 &= density,of,fluid,1 \ \rho_2 &= density,of,fluid,2 \end{align*}

Left hand side:

p_A =  p_1 + \rho_1g\Delta z_1

Right hand side:

p_{A'} = p_{at} + \rho_2g\Delta z_2

Equate and rearrange:

\begin{align*} p_1 + \rho_1g\Delta z_1 &= p_{at} + \rho_2g\Delta z_2 \ p_1-p_{at} &= g(\rho_2\Delta z_2 - \rho_1\Delta z_1) \ p_{1,gauge} &= g(\rho_2\Delta z_2 - \rho_1\Delta z_1) \end{align*}

If \rho_a << \rho_2:

\rho_{1,gauge} \approx \rho_2g\Delta z_2

Differential U-Tube Manometer

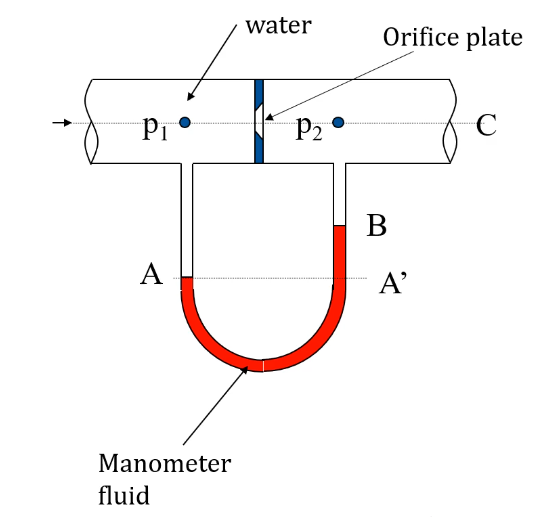
• Used to find the difference between two unknown pressures
• Can be used for any fluid that doesn't react with manometer fluid
• Same principle used in analysis

\begin{align*} p_A &= p_{A'} \ p_{bottom} &= p_{top} + \rho gh \ \rho_1 &= density,of,fluid,1 \ \rho_2 &= density,of,fluid,2 \end{align*}

Left hand side:

p_A = p_1 + \rho_wg(z_C-z_A)

Right hand side:

p_B = p_2 + \rho_wg(z_C-z_B)

Right hand manometer fluid:

p_{A'} = p_B + \rho_mg(z_B - z_a)

\begin{align*} p_{A'} &= p_2 + \rho_mg(z_C - z_B) + \rho_mg(z_B - zA)\ &= p_2 + \rho_mg(z_C - z_B) + \rho_mg\Delta z \ \ p_A &= p_{A'} \ p_1 + \rho_wg(z_C-z_A) &= p_2 + \rho_mg(z_C - z_B) + \rho_mg\Delta z \ p_1 - p_2 &= \rho_wg(z_C-z_B-z_C+z_A) + \rho_mg\Delta z \ &= \rho_wg(z_A-z_B) + \rho_mg\Delta z \ &= -\rho_wg\Delta z + \rho_mg\Delta z \end{align*}

Angled Differential Manometer

• If the pipe is sloped then

  p_1-p_2 = (\rho_m-\rho_w)g\Delta z + \rho_wg(z_{C2} - z_{C1})

• p_1 > p_2 as p_1 is lower

• If there is no flow along the tube, then

  p_1 = p_2 + \rho_wg(z_{C2} - z_{C1})

Exercise Sheet 1

1. If 4 m$^3$ of oil weighs 35 kN calculate its density and relative density. Relative density is a term used to define the density of a fluid relative

    \frac{35000}{9.81\times4} = 890 \text{ kgm}^{-3} 

   1000 - 891.9... = 108 \text{ kgm}^{-3}

2. Find the pressure relative to atmospheric experienced by a diver working on the sea bed at a depth of 35 m. Take the density of sea water to be 1030 kgm$^{-3}$.

   
   \rho gh = 1030\times 9.81 \times 35 = 3.5\times10^5
   

3. An open glass is sitting on a table, it has a diameter of 10 cm. If water up to a height of 20 cm is now added calculate the force exerted onto the table by the addition of the water.

   V_{cylinder} = \pi r^2h

   m_{cylinder} = \rho\pi r^2h

   W_{cylinder} = \rho g\pi r^2h = 1000\times9.8\pi\times0.05^2\times0.2 = 15.4 \text{ N} 

4. A closed rectangular tank with internal dimensions 6m x 3m x 1.5m high has a vertical riser pipe of cross-sectional area 0.001 m2 in
   the upper surface (figure 1.4). The tank and riser are filled with water such that the water level in the riser pipe is 3.5 m above the

   Calulate:

   i. The gauge pressure at the base of the tank.

   \rho gh = 1000\times9.81\times(1.5+3.5) = 49 \text{ kPa}

   ii. The gauge pressure at the top of the tank.

   > $$\rho gh = 1000\times9.81\times3.5 = 34 \text{ kPa}$$
   

   iii. The force exercted on the base of the tank due to gauge water pressure.

    > $$F = p\times A = 49\times10^3\times6\times3 = 8.8\times10^5 \text{ N}$$
   

   iv. The weight of the water in the tank and riser.

   > $$V = 6\times3\times1.5 + 0.001\times3.5 = 27.0035$$
   > $$W = \rho gV = 1000\times9.8\times27.0035 = 2.6\times10^5\text{ N}$$
   

   v. Explain the difference between (iii) and (iv).

   (It may be helpful to think about the forces on the top of the tank)

   The pressure at the top of the tank is higher than atmospheric pressure because of the riser. This means there is an upwards force on the top of tank. The difference between the force acting up and down due to pressure is equal to the weight of the water.

5. A double U-tube manometer is connected to a pipe as shown below.

   Taking the dimensions and fluids as indicated; calculate the absolute pressure at point A (centre of the pipe).

   Take atmospheric pressure as 1.01 bar and the density of mercury as 13600 kgm$^{-3}$.

   

   \begin{align*} P_B &= P_A + 0.4\rho_wg &\text{(1)}\ P_C = P_{C'} &= P_B - 0.2\rho_mg &\text{(2)}\ P_D = P_{at} &= P_A + 0.4\rho_wg &\text{(3)}\ \ \text{(2) into (3)} &\rightarrow P_B -0.2\rho_mg-0.1\rho_wg = P_{at} &\text{(4)}\ \text{(1) into (4)} &\rightarrow P_A + 0.4\rho_wg - 0.2\rho_mg - 0.1\rho_wg = P_{at} \ \ P_A &= P_{at} + 0.1\rho_wg + 0.2\rho_mg - 0.4\rho_wg \ &= P_{at} + g(0.2\rho_m - 0.3\rho_w) \ &= 1.01\times10^5 + 9.81(0.2\times13600 - 0.3\times1000)\ &= 124.7\text{ kPa} \end{align*}

Submerged Surfaces

Prepatory Maths

Integration as Summation

Centroids

• For a 3D body, the centre of gravity is the point at which all the mass can be considered to act
• For a 2D lamina (thin, flat plate) the centroid is the centre of area, the point about which the lamina would balance

To find the location of the centroid, take moments (of area) about a suitable reference axis:

moment\,of\,area = moment\,of\,mass

(making the assumption that the surface has a unit mass per unit area)

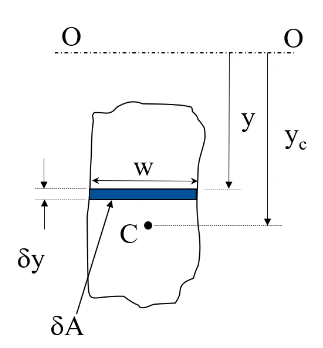
moment\,of\,mass = mass\times distance\,from\,point\,acting\,around

Take the following lamina:

1. Split the lamina into elements parallel to the chosen axis

2. Each element has area \delta A = w\delta y

3. The moment of area (\delta M) of the element is \delta Ay

4. The sum of moments of all the elements is equal to the moment M obtained by assuing all the area is located at the centroid or:

   Ay_c = \int_{area} \! y\,\mathrm{d}A

   or:

   y_c = \frac 1 A \int_{area} \! y\,\mathrm{d}A

   • \int y\,\mathrm{d}A is known as the first moment of area

Example 1

Determine the location of the centroid of a rectangular lamina.

Determining Location in y direction

1. Take moments for area about OO

   \delta M = y\delta A = y(b\delta y)

2. Integrate to find all strips

   M = b\int_0^d\! y \,\mathrm{d}y = b\left[\frac{y^2}2\right]_0^d = \frac{bd^2} 2

   (b can be taken out the integral as it is constant in this example)

   but also $$M = (area)(y_c) = bdy_c$$

   so $$y_c = \frac 1 {bd} \frac {bd} 2 = \frac d 2$$

Determining Location in x direction

1. Take moments for area about O'O':

   \delta M = x\delta A = x(d\delta x)

2. Integrate

   M_{O'O'} = d\int_0^b\! x \,\mathrm{d}x = d\left[\frac{x^2} 2\right]_0^b = \frac{db^2} 2

   but also $$M_{O'O'} = (area)(x_c) = bdx_c$$

   so $$x_c = \frac{db^2}{2bd} = \frac b 2$$

Horizontal Submereged Surfaces

Assumptions for horizontal lamina:

• Constant pressure acts over entire surface of lamina
• Centre of pressure will coincide with centre of area
• total\,force = pressure\times area

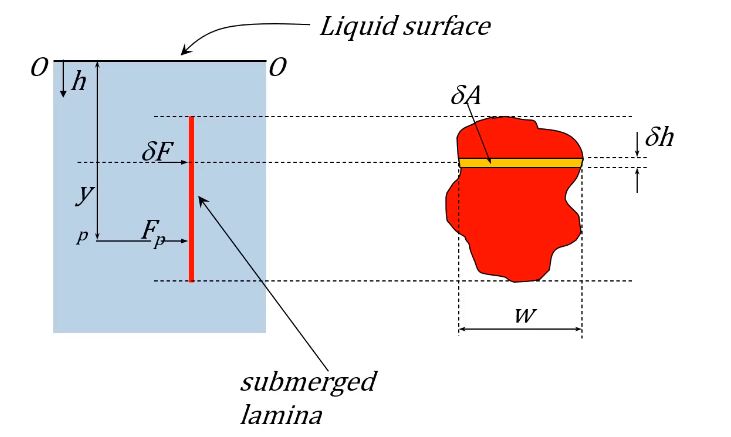
Vertical Submerged Surfaces

• A vertical submerged plate does experience uniform pressure
• Centroid of pressure and area are not coincident
• Centroid of pressure is always below centroid of area for a vertical plate
• No shear forces, so all hydrostatic forces are perpendicular to lamina

Force acting on small element:

\begin{align*} \delta F &= p\delta A \ &= \rho gh\delta A \ &= \rho gh w\delta h \end{align*}

Therefore total force is

F_p = \int_{area}\! \rho gh \,\mathrm{d}A = \int_{h_1}^{h_2}\! \rho ghw\,\mathrm{d}h

Finding Line of Action of the Force

\begin{align*} \delta M_{OO} &= \delta Fh = (\rho gh\delta A)h \ &= \rho gh^2\delta A = \rho gh^2w\delta h \ \ M_{OO} &= F_py_p = \int_{area}! \rho gh^2 ,\mathrm{d}A \ &= \int_{h1}^{h2}! \rho gh^2w ,\mathrm{d}h \ \ y_p = \frac{M_{OO}}{F_p} \end{align*}