notes/mechanical/mmme1029_materials.md

author	date	title	tags
Alvie Rahman	\today	MMME1029 // Materials	uni nottingham mechanical engineering mmme1029 materials

\tableofcontents

Lecture 1 (2021-10-04)

1A Reading Notes

Classification of Energy-Related Materials

• Passive materials---do not take part in energy conversion e.g. structures in pipelines, turbine blades, oil drills

• Active materials---directly take part in energy conversion e.g. solar cells, batteries, catalysts, superconducting magnests

• The material and chemical problems for conventional energy systems are mostly well understood and usually associated wit structural and mechanical properties or long standing chemical effects like corrosion:

  • fossil fuels
  • hydroelectric
  • oil from shale and tar
  • sands
  • coal gasification
  • liquefaction
  • geothermal energy
  • wind power
  • bomass conversion
  • solar cells
  • nuclear reactors

Applications of Energy-Related Materials

High Temperature Materials (and Theoretical Thermodynamic Efficiency)

• Thermodynamics indicated that the higher the temperature, the greater the efficiency of heat to work:

   \frac{ T_{high} - T_{low} }{ T_{high} } 

• The first steam engines were only 1% efficient, while modern steam engines are 35% efficient primarily due to improved high-temperature materials.

• Early engines made from cast iron while modern engines made from alloys containing nickel, molybdenum, chromium, and silicon, which don't fail at temperature above 540 \textdegree{}C

• Modern combustion engines are nearing the limits of metals so new materials that can function at even higher temperatures must be found--- particularly intermetallic compounds and ceramics are being developed

Types of Stainless Steel

• Type 304---common; iron, carbon, nickel, and chromium
• Type 316---expensive; iron, carbon, chromium, nickel, molybdenum

Self Quiz 1

1. What is made of billion year old carbon + water + sprinkling of stardust?

   Me

2. What are the main classifications of materials?

   Metals, glass and ceramics, plastics, elastomers, polymers, composites, and semiconductors

3. [There are] Few Iron Age artefacts left. Why?

   They rusted away

4. What is maens by 'the micro-structure of a material'?

   The very small scale structure of a material which can have strong influence on its physical properties like toughness and ductility and corrosion resistance

5. What is a 'micrograph' of a material?

   A picture taken through a microscope

6. What microscope is used to investage the microstructure of a material down to a 1 micron scale resolution?

   Optical Microscope

7. What microscope is used [to investigate] the microstructure of a material down to a 100 nm scale resolution?

   Scanning Electron Microscope

8. What length scales did you see in the first slide set?

   1 mm, 0.5 mm, 1.5 \textmu{}m

9. What material properties were mentioned in the first slide set?

   Hardness, brittleness, melting point, corrosion, density, thermal insulation

Self Quiz 2

1. What is the effect of lowering the temperature of rubber?

   Makes it more brittle, much less elastic and flexible

2. What material properties were mentioned in the second slide set?

   Young's modulus, specific heat, coefficient of thermal expansion

Lecture 2

Properties of the Classes

Metals

• Ductile (yields before fracture)
• High UFS (Ultimate Fracture Stress) in tension and compression
• Hard
• Tough
• High melting point
• High electric and thermal conductivity

Ceramics and Glasses

• Brittle --- elastic to failure, no yield
• Hard (harder than metals)
• Low UFS under tension
• High UFS under compression
• Not tough
• High melting points
• Do not burn as oxide ceramics are already oxides
• Chemically resistant
• Poor thermal and electric conductivity
• Wide range of magnetic and dielectric behaviours

Polymers

• Organic---as in organic chemistry (i.e. carbon based)

• Ductile

• Low UFS in tension and compression

• Not hard

• Reasonably tough

• Low threshold temperature to charring and combustion in air or pure oxygen

• Low electrical and thermal conductivity

  • There are some electrically conductive polymers

Composites

• Composed of 2 or more materials on any scale from atomic to mm scale to produce properties that cannot be obtained in a single material

  • Larger scale mixes of materials may be called 'multimaterial'

• Material propertes depends on what its made of

Terms

Organic vs Inorganic Materials

• Organic materials are carbon based
• From chemistry, organic compounds are ones with a C-H bond
• Inorganic compounds do not contain the C-H bond

Crystalline vs Non-Crystalline Materials

• Most things are crystalline

  • Ice
  • Sugar
  • Salt
  • Metals
  • Ceramics

• Glasses are non-crystalline

Material Properties

Density

\rho = \frac m v

• Density if quoted at STP (standard temperature and pressure---298 K and 1.013\times 10^5 Pa)

• Metals, ceramics, and glasses are high density materials

• Polymers are low density

• Composites span a wide range of density as it depends on the materials it is composed of

  e.g. composites with a metal matrix will have a much higher density than those with a polymer matrix

Melting Points

• Measured at standard pressure and in an intert atmosphere (e.g. with Nitrogen, Argon, etc)

  • Diamond and graphite will survive up to 4000 \textdegree{}C in an inert atmosphere but would burn at around 1000 \textdegree{}C in oxygen

• High melting points -> high chemical bond strength

Corrosion

• It's not just metals that corrode

• Polymers

  • UV degradation
  • Water absorption can occur in degraded polymers

• Glass

  • Leaching
  • Sodium ions can leave the glass when covered in water. If the water stays, the high pH water can damage the class

Self Quiz

Consolidation Questions 1

i. Metal ii. Titanium

2. i. Polymer ii. Polyester

i. Ceramic ii. Alumino-silicate

i. Composite ii. GFRP or CFRP

i. Metal ii. Aluiminium alloy

i. Metal ii. Aluiminium alloy

i. Polymer ii. Acrylic

i. Ceramimc ii. Glass

i. Composite ii. Concrete

Consolidation Questions 2

C B

Polymers

Introduction to Polymers

There are 3 types of polymers:

• thermoplastics

  

  No cross links between chains. The lack of cross links allows recycling of polymers by heating it above the glass transition material, T_g, lowering the viscosity.

  An example of thermoplastics is PET, used in water bottles

• thermosets

  

  has lots of cross-links between chains, making it more rigid. Heating does not lower its viscosity making them much harder/impossible to recycle.

  and example of thermosets is melamine formaldehyde, used on kitchen tabletops

• elastomers

  

  has some cross links and a lot of folding of chains

  Latex is an example of an elastomer

Polymers are relatively new materials, lightweight, durable, flammable, and degraded by UV light. They are made of long carbon-carbon chains.

Stress-Strain Curve of Polymers

Thermoplastics

The simplest polymer is poly(ethene):

When 2 polymer chains get close together, Van der Waals (vdw) forces keep them together. vdw forces are very weak, much weaker than the covalent bonds inside the polymer.

Stress Strain Curve

• During linear deformation, the carbon chains are strethed.
• At yield stress, the carbon chains get untangled and slide past eache other.
• Necking initially allows the chains to slide at lower stress.
• As the chains pull, align, and get closer, the vdw forces get stronger and more stress is required to fracture.

Crystalline and Amorphous/Glassy Solids (Heating and Cooling)

Amorphous Thermoplastics

• As you heat above T_g, the chains get easier to move past each other.
• It is known as an amorphous supercooled liquid.
• There is not really a melting point are there are no crystals, but T_m is the point where the chains are easy to move

Crystalline Polymers

• The glass transition point does not exist for crystalline polymers
• The solid is difficult to deform below T_m and is not ductile
• Above T_m the chains are very easy to move past each other

Semi-Crystalline

• Below T_g, only local movements in chains are possible, so the material is less ductile. The solid crystalline regions makes it difficult to move the chains.
• Between T_g and T_m, the glassy chains are easier to move but the crystalline regions remain difficult
• Above T_m the chains easily move past each other

Specific Volume vs Temperature

Path ABCD

• a-b --- Start cooling the true liquid
• b-c --- At the freezing point, T_m, the true liquid freezes diretly to a crystalline solid
• c-d --- The crystalline solid cools t room temperature as the temperature is lowered

Path ABEF

• a-b --- start cooling the true liquid

• b --- at the freezing point nothing freezes

• b-e --- the liquid becomes supercooled and contracts and becomes more viscous as the temperature decreases.

  The supercooled liquid region is between T_g and T_m

  Supercooling requires you to cool the sample quicker than you would for path ABCD

• e --- T_g is reached and the supercooled liquid sets to a amorphous solid

• e-f --- the amorphous solid cools from room temperature and contract as the temperature is lowered

Relative Molar Mass and Degree of Polymerisation

• Number Average RMM --- \bar M_n = \sum x_iM_i
• Weight Average RMM --- \bar M_w = \sum w_iM_i
• Degree of polymerisation --- n_n = \frac {\bar M_n} m and n_w = \frac {\bar M_w} m

where

• M_i is the RMM of the chain
• x_i is the fraction of the polymer that is composed of that chain by number/quantity
• w_i is the fraction of the polymer that is composed of that chain by mass/weight
• m is the RMM of the monomer from which the polymer was made

Making Polymers

There are two ways to make polymers:

• Addition Poymerisation
• Condensation Polymerisation

Elastic Deformaion

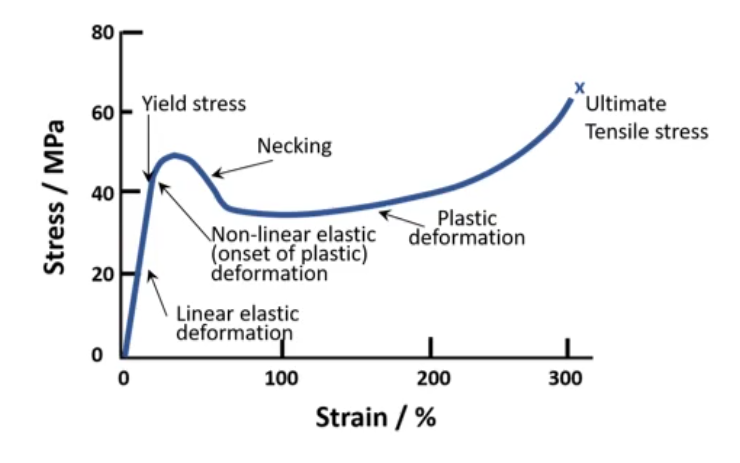
Elastic deformation is deformation where the material will return to original shape after the applied stresses are removed.

Elastic deformation is the first type of deformation that happens when stresses are applied to a material and is represented by the straight line at the beginning of a stress-strain curve.

Modulus of Resillience (E_r)

This is the area under the elastic portion of a stress-strain graph of a material.

Plastic Deformation

Toughness (Absorbing Energy Through Plastic Deformation)

• The toughness of a material is its ability to absorb energy through plastic deformation without fracturing
• The material toughness of a ductile material can be determined by finding the area under its stress-strain curve (e.g. by integrating the graph)
• Brittle materials like ceramics and glasses exhibit no material toughness
• Ductile materials have a possibility of achieving large material toughness

Ductility measures how much something deforms plastically before fracture, but just because a material is ductile does not make it tough.

The key to high material toughness is a good combination of large ultimate fracture stress and large ductility.

• The unit of toughness is energy per unit volume as toughness can be mathematically expressed as:

  toughness = \int^{\varepsilon_f}_0\! \sigma \,\mathrm{d}\varepsilon 
    = \frac{\text{Energy}}{\text{Volume}} $$
  
  

• A metal may have satisfactory toughness under static loads but fail under dynamic loads or impact

  This may be caused by the fact that ductility and toughness usually decrease as rate of loading increases.

• Ductility and toughness decreasee with temperature

• Notches in the material affect the distribution of stress in the material, potentially changing it from a uniaxial stress to multiaxial stress

Charpy Impact Test

Measures material toughness by determining the amount of energy absorbed during fracture.

It works by essentially dropping a hammer into a sample whose dimensions are standardized (usually either by BSI or ISO) and measuring how high the hammer goes up on the other side, after it breaks the material

The height of the hammer after impact will tell you how much enery is left in it, and therefore how much has been aborbed by the now broken sample.

Under a microscope, more ductile fractures appear fibrous or dull, whereas less ductile surfaces have granular or shiny surface texture.A

The charpy test has a couple issues:

• Results are prone to scatter as it is difficult to achieve a perfectly shaped notch
• Temperature has to be strictly controlled since it affects a material's ductility

The setup of a charpy impact test

1. Sample is made to standardized dimensions, with a notch
2. Sample is placed on support
3. A very heavy hammer pendulum of mass m is dropped from rest at h_0 to swing about a pivot, reaching E_{kmax} vertically below the pivot.

a. If no sample is in place then the hammer will swing back up on the other side to a height of h_h where theoretically $h_h = h_0$ b. With a sample placed vertically below, some of the E_k is transferred to the sample to bend and (usually) break the sample.

  If breaks the sample, it will swing up to the other side, where its max height, $h_f$ can be
  used to calculate how much energy was used to break the sample:

  $$E = mg(h_h-h_f)$$

  Where $g$ is acceleration due to gravity.

Ductility

Ductility is the plastic deformation a material withstands before fracture.

Griffith Surface Flaws

These flaws vary in size and shape. They limit the ability of any material, brittle or ductile, to withstand tensile stresses as they concentrate the tensile forces applied to a smaller area.

The stress at the tip of the flaw:

\sigma_{actual} = 2\sigma\sqrt{\frac a r}

For deep (a is large) or thin (r is small) the stress is magnified and, if it exceeds the UFS in a brittle material, the flaw will grow into a crack, resulting in the brittle material fracturing.

However in a ductile material, the tip of the flaw can heal, reducing a and increasing r. This is due to the chemical structure of ductile materials like metals.

Stress Intensity Factor

Stress Intesity Factor, K:

K = f\sigma\sqrt{\pi a}

where:

• f is the geometry factor (1 would represent an infinite width sample, and 0 a 0 width sample)
• \sigma is applied tensile strength
• a is flaw depth

Fracture Toughness

The value of K that causes the notch to grow and cause fractures. This is value is known as the fracture toughness, K_c.

At low thicknesses fracture toughness depends on thickness but as thickness increases, $K_c$ decreases to the constant value, the plane strain fracture toughness, K_{1c}.

Composites

Composites are made of two or more materials, which when combined together, at up to a milimetre scale, have superior properties to their parent materials.

Composites tend to be 2-phase: a dispersed phase in a matrix. The disepersed phase tends to be fibres (large aspect ratio) or particles (low aspect ratio) which are embedded in a matrix, which are often resins.

Composite properites are affected by the dispersed phase geometry:

• Shape
• Size
• Distribution
• Relative orientation (for fibres)

Rule of Mixtures

E_c lies between the arithmetic mean (upper limit):

V_mE_m + E_pV_p

and the geometric mean (lower limit):

\frac{V_mE_mE_pV_p}{V_mE_m + E_pV_p}

Where E_c, E_m, E_p are the Young's moduluses of the composite, matrix, and particles, respectively, and V_m and V_p are the volume of the matrix and particles, respectively.

Particle Reinforced Composites

Applications of Composites

Tungsten Carbide Cobalt for Cutting Tools

The Tungest Carbide (WC) particle are a truly brittle ceramic. They are very hard but the brittleness means they are easy to break.

The solution is to hold small WC particles in a ducitle metal matrix. In this case it is Cobalt (Co).

This way, crack in one WC particle does not necessarily mean other particles are broken, meaning the cutting tool overall still works.

Another advantage of this composite is that WC is not very thermally conductive and has a high melting point, which allows it to work well the environment it's in.

Resin Bonded Alumina for Sanding Disks

This is another example of brittle but hard ceramics being put in a ductile matrix. In this case it's a resin.

It follows the same idea---separating the ceramics into small particles means the particles can break and the product still works overall, as there are thousands of particles which are not broken.

Fibre Reinforced Composites

Specific Property

Specific Property of a composite is a property divided by density of composite. Here are some examples of specific properties:

• Specific ultimate tensile stress = \frac{\sigma_{UTS}}{\rho_c}
• Specific Young's modulus/stiffness = \frac{E_c}{\rho_c}

Influence of the Fibres

Depends on:

• Fibre type
• Fibre length and diameter
• Fibre orientation
• Strength of bond between fibre and matrix

Stress Strain Graph of a Fibre Reinforced Composite

Note that the composite fails at the same strain as the fibres but yields at the same strain as the polymer matrix.

The elastic behaviour of the composite before yielding is dependent on the strength of the chemical bonds between the surface of the fibre and matrix.

Mechanical Performance of a Fibre Reinforced Composite

• Stress/strain behaviour of fibre

• Stress/strain behaviour of matrix

• Fibre volume fraction

• Applied stress direction

  Longitudinal is along direction of fibres, transverse is 90\textdegree to direction.

  Fibre composites tend to be much much weaker in transverse direction:

  Composite	Longitudinal UTS	Transverse UTS
  GF/PET	700	20
  CF/Epoxy	1000	35
  Kevlar/Epoxy	1200	20

  (All units in MPa)

Thermal Properties of Materials

Specific Heat Capacity

How much heat energy is required to raise the temperature of a body by one unit:

 C_p = \frac{\Delta E}{m\Delta T} 

where c is specific heat capacity.

It is measured at a constant pressure, usually 1.013\times 10^5 Pa.

Molar Heat Capacity

C_pm = \frac{\Delta E}{n\Delta T}

What is a mole?

The mole (symbol: mol) is the base unit of amount of substance in the International System of Units (SI). It is defined as exactly 6.02214076\times 10^{23} elementary entities ("particles")

~ Wikipedia: Mole (unit)

How Much Does a mol of Something weigh?

A mol of an element weighs its relative atomic mass (A_r) but in grams. For example, Carbon-12 has an A_r of 12 (as it's made of 6 neutrons, 6 protons, and 6 electrons which have negligible mass) so a mol of Carbon-12 has a mass of 12 g.

Thermal Expansion

Origin of Thermal Expansion

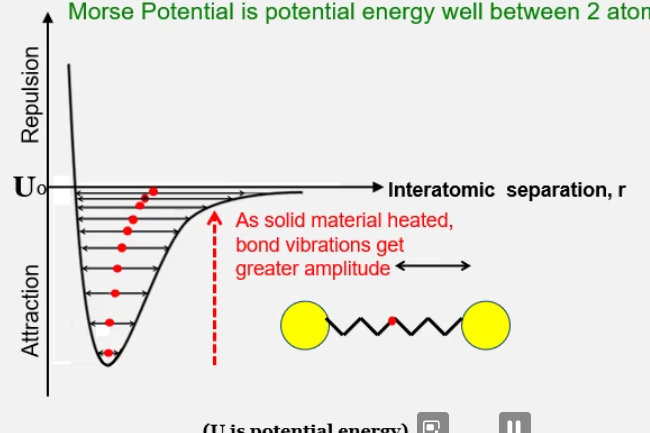
All atomic bonds vibrate, on the magnitude of gigahertz. The bonds vibrate about a mean positoin and the vibration is a simple harmonic motion.

From the graph below you can see that as energy (in the form of heat) is supplied to the bonds, the amplitude of the vibrations get larger and larger. You can also see the mean position of the bond gets further and further away, meaning the volume of the material also is increasing. The mean position of the bond is what dictates the volume, as this means the inter-atomic separation increases.

Morse potential is the energy well between 2 bonded atoms. The graph is asymmetric due to the repulsion experienced by atoms as they apporach.

Linear Coefficient of Thermal Expansion

\alpha_L = \frac{\Delta L}{L_0 \Delta T}

where L is the sample length.

Example 1

A 1 m long bar of aluminium metal cools in the solid state from 660 \textdegree{}C to 25 \textdegree{}C.
Calculate the length of the bar after it cools down, given \alpha_L = 25\times10^{-6} K$^{-1}$.

\begin{align*} l_0 &= 1 \ \Delta T &= T_f - T_0 = 25 - 660 = -635 \ \ \alpha_L &= \frac{l_f - l_0}{l_0 \Delta T} \ \alpha_L l_0 \Delta T &= l_f - l_0 \ l_f &= \alpha_L l_0 \Delta T + l_0 = 0.984 \end{align*}

Linear Thermal Expansion and Isotropism

Since isotropic solids have the same properties in all directions, you can say that for an isotropic solid:

\alpha_V = 3\alpha_L = \frac{\Delta V}{V_0 \Delta T}

Reasons to Care About Thermal Expansion

• A coating on a material may fail if the thermal expansion coefficients do not match
• A brittle material may thermally shock and fracture due to thermal expansion mismatch between the ouside and inside, especially if the material is not very thermally conductive

Thermal Conductivity

Thermal conductivity is the rate at which heat power is transferred through a material.

\frac{Q}{A}  = k \frac{\Delta T}{\Delta x}

where Q is heat power, A is area of the surface, \frac{\Delta T}{\Delta x} is the temperature gradient, and k is the thermal conductivity constant.

Origin of Thermal Conductivity

Heat is transferred through materials by electrons (and partially by atomic vibrations)

Metals have high thermal conductivity as their delocalised 'sea' electrons are about to move about easily. This makes them excellent conductors of heat and electricity.

Ceramics, glasses, and polymers do not have delocalised electrons and are therefore poor conductors of heat and electricity (they are insulators).

Polymer foams are even better insulators because they have holes which lowers their density.

Chemical Bonding of Materials

Chemical bonds are what holds a material together in solid state. There are 5 main types of bonds:

Type	Dissociation energy
Ionic	600 to 1500
Covalent	300 to 1200
Metallic	100 to 800
Hydrogen	4 to 23
vdw	0.4 to 4

The dissociation energy is the energy required to break the bond, or the strength of the bond.

Materials and their Properties and Bonding

Ceramics and Glasses

Ceramics and glasses are composed of mixed ionic and covalent bonding. Their strong and rigid bonds have no ability to slide past each other. This makes the materials brittle.

Metals

Metals are based on metallic bonding (woah). This type of bonding does allow for ions to slide past each other, making metals ductile.

Polymers

Polymer chains made of C-C covalent bonds are strong, like those found in ceramics.

However, in thermoplastics polymers, the materials can yield by having the chains untangle and then align, as the chains slide past each other. This means that stronger bonds between polymer chains means a higher yield stress in thermoplastic polymers.

Crystallisation of Materials

Atomic Arrangement

• No order

• Short range order

  Silica glasses have short range order on the atomic scale. They are composed of regular SiO$_4$ units which all have the same bond length and bond angles.

  However, these units bond together irregularly, which results in different length chemical bonds and angles between the units, meaning they do not have any long range order.

• Long range order

Cubic Unit Cells

• Lattice Parameter --- One side of a unit cell

  The lattice parameter can be different for each side of a cell.

• Simple cubic unit (SC):

  

  Lattice Parameter = 2r

• Face centred cubic (FCC)

  

• Body centred cubic (BCC)

  

Packing Factor

\text{packing factor} = \frac{\text{ions per unit cell} \times V_{ion}}{V_{cell}}

Theoretical Density

\text{theoretical density} = \frac{\text{ions per unit cell} \times m_{ion}}{V_{cell}}

Polymorphism

Example of a polymorphic solid-state phase transfomration of iron at 1185 K and 1 atm:

\text{Fe}_{\text{BCC}} \longleftrightarrow \text{Fe}_{\text{FCC}}

Below 1185 K and at 1 atm, only BCC exists. Above 1185 K and at 1 atm, only FCC exists.

Points, Directions, Planes in a Cubic Unit Cell

Slip Systems in Metals

Metal ions lying in close-packed planes and directions move more easily, increasing ductility. The combination of a close packed plane and direction is called a slip system.

A close packed direction is where ions touch all the way along the direction.

A close packed plane is where ions touch all the way on a plane.

FCC metal ductility is mainly controlled by the (111) slip plane

X-Ray Diffraction (Bragg's Law)

The wavelength of x-rays, \lambda, is roughly equal to the distance, d, between atom/ion layers. This allows x-rays to probe for d via Bragg's Equation:

Requirements for the x-rays:

• Monochromatic
• Coherent (phase difference of 2\pi n where n is any integer)
• Parallel with each other

The incoming x-rays 1 and 2 strike the rows of ions in the crystal and are diffracted, which can be considered reflection at the atomic level. The angle of incidence equals the angle of reflection.

The outgoing x-rays 1 and 2 are coherent only if the extra path travelled by ray 2, $2d\sin\theta$ is any multiple, n, of \lambda. Or:

n\lambda = 2d\sin\theta

This is Bragg's Law.