notes/uni/mmme/2047_thermodynamics_and_fluid_dynamics/pumps.md

author	date	title	tags	uuid	lecture_slides	lecture_notes	exercise_sheets
Akbar Rahman	\today	MMME2047 // Turbomachinery // Pumps	turbomachinery pumps	11f0f745-2364-4594-8e47-127a4af39417	./lecture_slides/T5 - Turbomachinery - with solutions.pdf	./lecture_notes/turbomachinery lecture notes(H Power).pdf	./exercise_sheets/Turbomachinery-problems.pdf

Turbomachinery are rotating devices that add (pump for liquids; fan, blower, or compressor for gases at <0.02, <1 bar, and > 1 bar respectively) or extract (turbine) energy from a fluid.

Errata

Worked Example 3 Diameter Incorrect (lecture slides 42, lecture notes p. 13)

Question specifies 21" diameter, but should be 32" diameter I think?? Solution provided in lecture slides continues to use 21" dia, but measures from graph as if is 32". Weird.

Positive Displacement (PD) Pumps

• PD pumps force fluid along using volume changes (e.g. bike pumps, the heart)
• All PD pumps deliver a periodic flow
• They deliver any fluid regardless of viscosity (dynamic pumps struggle with viscous fluids)
• They are self priming (will be filled automatically)
• They can operate under high pressures (300 atm) but low flow rates (25 m$^3$h$^{-1}$)
• flow rate can be only be changed by vary speed or displacement

Dynamics Pumps

• add momentum to fluid by fast moving blades or vanes

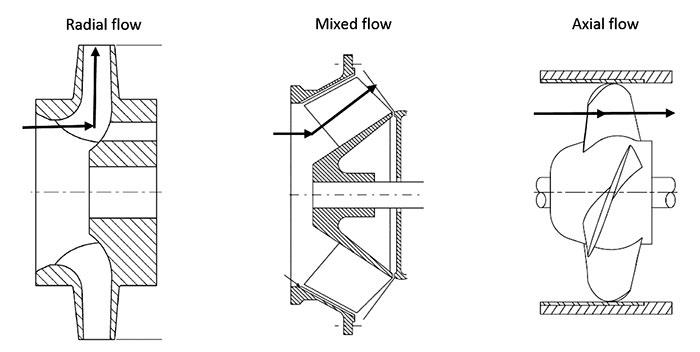
• classified based on direction of flow at exit:

  • centrifugal
  • axial
  • mixed flow

• fluid increases momentum while moving through open passages and extra velocity is converted to pressure through exiting it into a diffuser section

• provide high flow rates (up to 70000 m$^3$h$^{-1}$) but usually at moderate pressure rises (a few atm)

• require priming

Centrifugal Pumps

• fluid enters through eye of casing and gets caught in impeller blades
• fluid is whirled outwards until it leaves via the expanding area section, known as the diffuser or volute

Blades

• backward inclined blades - most common and efficient, intermediate pressure rise, less robust
• straight blades - simplest geometry, high pressure rise, less robust
• forward inclined blades - more blades but smaller, lowest pressure rise, lowest efficiency, more robust

Integral Analysis of Centrifugal Pumps

Derivation in slides (p. 23-25).

\begin{align} \frac{w_s}{g} - \left(\frac{u_2-1-q}{g}\right) &= \left(\frac{p_2}{\rho g} + z_2 + \frac{v_2^2}{2g}\right) -\left(\frac{p_1}{\rho g} + z_1 + \frac{v_1^2}{2g}\right) \ H_s - H_f &= H = H{T,2} - H_{T,1} \nonumber \end{align}

where H_s is supplied head to pump, H_f friction loss head, H is head supplied to fluid, H_{T,1} is total head at inlet, and H_{T,2} is total head at outlet.

Assuming that z_1 \approx z_2, v_1 \approx v_2 (from inlet and outlet diameters are equal) then:

\begin{equation} H \approx \frac{p_2-p_1}{\rho g} \end{equation}

and the power to the fluid (water horsepower) is:

\begin{equation} P_w = \rho QgH \end{equation}

where Q is volumetric flow rate.

Power supplied to the pump (brake horsepower), P = \omega T, lets us find the overall pump efficiency:

\begin{equation} \eta = \frac{P_w}{P} = \frac{\rho QgH}{\omega T} = \eta_h \eta_m \eta_v \end{equation}

where:

• \eta_h = 1 - \frac{H_f}{H_s} is hydraulic efficiency
• \eta_m = 1- \frac{P_f}{P} is mechanical efficiency
• \eta_v = \frac{Q}{Q+Q_L} (where Q_L is loss due to leakage flow) is the volumetric efficiency

Performance

Cavitation

Cavitation is when bubbles form in liquid by sudden pressure drop, followed by their implosion when original pressure is restored. The implosion generates a high pressure wave that can damage nearby solid surfaces.

In a centrifugal pump, the fluid pressure drops at the impeller's eye, where it has the minimum value. If pressure falls below saturation pressure, bubbles appear. Pressure grows as the fluid flows between the blades as the ducts are diverging. Pressure is maximum at the trailing edge of the blades, on their front side. This is where cavitation occurs and causes wear on the blade.

https://www.michael-smith-engineers.co.uk/resources/useful-info/pump-cavitation
https://www.youtube.com/watch?v=g1o5Z9o7b0
https://www.youtube.com/watch?v=eMDAw0TXvUo
https://www.youtube.com/watch?v=1Lbxtjfdat4

Net Positive Suction Head (NPSH)

The following conditions must be satisfied to prevent cavitation:

\begin{equation} H_i - \frac{p_v}{\rho g} > \text{NPSH} \end{equation}

where H_i = \frac{p_i}{\rho g} + \frac{v_i^2}{2g} is total head at inlet, p_v is saturation pressure at T_i.

It is important that the inlet pressure is as high as possible. To do this, one can reduce frictional losses (e.g. shorter smoother pipes) or install the pump lower down (even below the reservoir) (slides p. 36).

Dimensionless Pump Performance

Output variables for a pump's performance are pump head H and brake horsepower P. Input variables are discharge Q, impeller diameter D, and shaft speed n.

The dimensional relationships that we need are

gH = f_1(Q, D, n, \rho, \mu, \epsilon)

P = f_2(Q, D, n, \rho, \mu, \epsilon)

Pi-theorem allows the following coefficients to be derived:

\begin{align} \Pi_1 &= C_H = \frac{gH}{n^2D^2} &\text{Head coefficient} \ \Pi_2 &= C_P = \frac{P}{\rho n^3D^5}&\text{Power coefficient} \ \Pi_3 &= C_Q = \frac{Q}{nD^3}&\text{Capacity coefficient} \ \Pi_4 &= \text{Re} = \frac{\rho nD^2}{\mu}&\text{Reynolds Number} \ \Pi_5 &= = \frac{\epsilon}{D}&\text{Roughness Parameter} \end{align}

Therefore it can be expressed that:

\begin{align*} C_H &= g_1\left(C_Q, \text{Re}, \frac{\epsilon}{D}\right) \ C_P &= g_2\left(C_Q, \text{Re}, \frac{\epsilon}{D}\right) \end{align*}

However for pumps it is assumed that Reynolds number and roughness parameter are constant for a set of similar pumps:

Similar pumps are those which have the same design, other than the dimensions. Therefore it can be written that:

\begin{align*} C_H &\approx g_3(C_Q) \ C_P &\approx g_4(C_Q) \end{align*}

Pump efficiency is already dimensionless but can be related to the other dimensionless groups:

\eta = \frac{C_HC_Q}{C_P} \approx \eta(C_Q)

A nondimensional NPSH can also be defined:

C_{HS} = \frac{g\cdot\text{NPSH}}{n^2D^2} \approx C_{HS}(C_Q)

However, larger impellers for similar pump designs can lead to higher efficiencies, higher Reynolds number, lower friction head, and lower leakage low.

Mixed and Axial Flow Pumps

Centrifugal pumps are high-head, low discharge machines, and therefore not suitable when high flow rates are required.

For high flow rates, mixed-flow and axial-flow pumps are preferred. The flow passes through the impeller with an axial flow component and less centrifugal component.

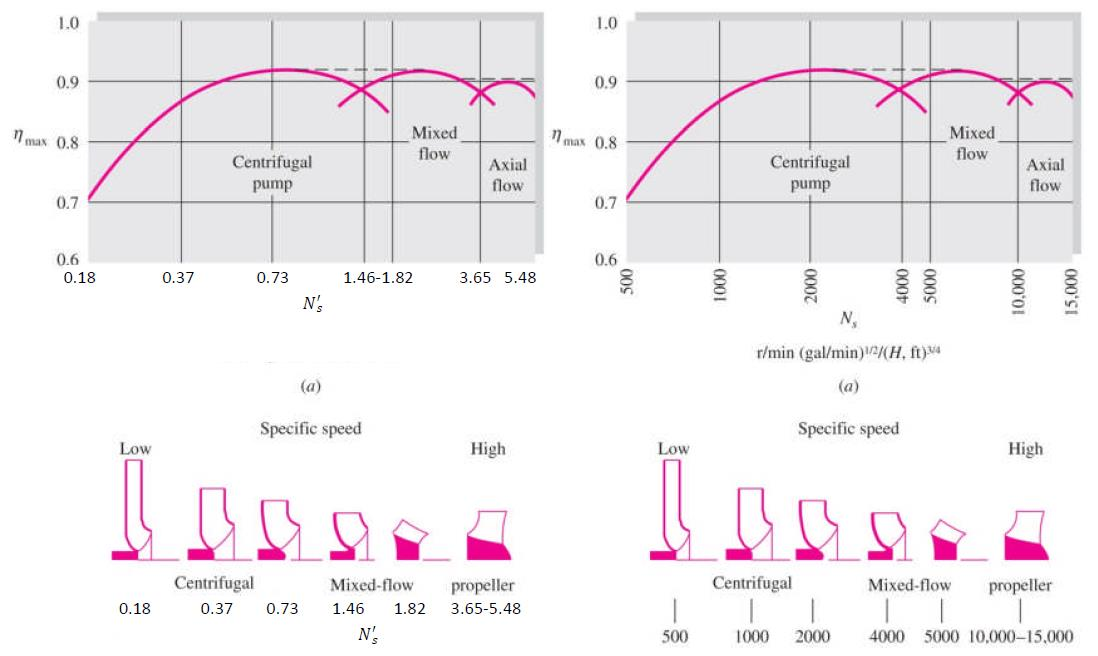
Specific Speed

Specific speed is a nondimensional shaft speed which is obtained by eliminating the diameter between C_Q and C_H:

N'_S = \frac{C_Q^{\frac12}}{C_H^{\frac34}}

There is also 'lazy' dimensional version which may be used by manufacturers:

N'_S = \frac{N_S}{2734}

where N_S is the 'lazy' dimensional version, N'_S is the dimensionless version.