notes/uni/mmme/2051_electromechanical_devices/piezoelectrics.md

author	date	title	tags	uuid	lecture_slides	lecture_notes	exercise_sheets
Akbar Rahman	\today	MMME2051 // Piezoelectrics	piezoelectrics op_amps	ed7d0899-478d-4f0d-b0e9-634cdbb5b48a	./lecture_slides/MMME2051EMD_Lecture7.pdf		./seminar_worksheets/MMME2051_Lec7_Top1_Quiz.pdf ./seminar_worksheets/StrainGaugeHomework.pdf

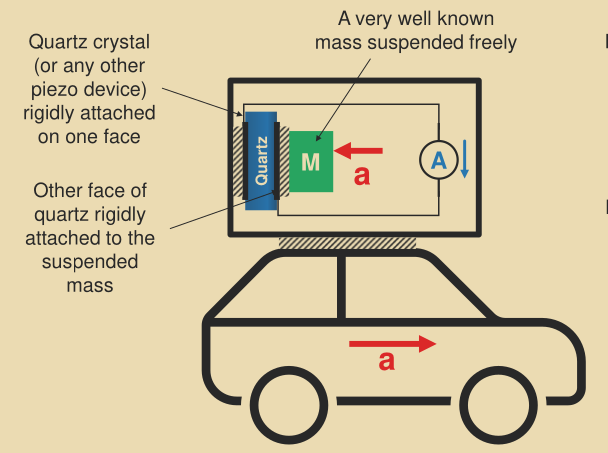
Piezoelectricity is the charge that gets accumulated in some materials upon application of mechanical stress

Q \propto F

This relation allows the measurement of force using electric signals.

\begin{align*} Q &\propto F \ Q &= k_1F \ &= k_1Ma \ \frac{\mathrm d Q}{\mathrm dt} &= i = k_1M\frac{\mathrm da}{\mathrm dt} \end{align*}

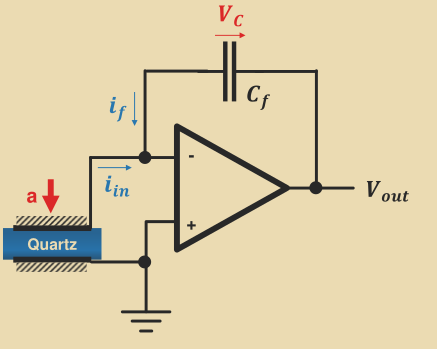
Integrating Amplifier

Measuring current is expensive and difficult. Integrating the current helps to measure a voltage instead, which is easier. This is done using the following amplifier:

\begin{align*} V_\text{out} &= A_{OL}(V^+-V__) = -A_{OL}V__ \ V__ &= V_\text{out} - V_C \end{align*}

As input resistance of op amp is infinite:

i_f = -i_n = -k_1M\frac{\mathrm da}{\mathrm dt}

From the capacitor equation:

i_f = C_f \frac{\mathrm dV_C}{\mathrm dt} = -k_1M\frac{\mathrm da}{\mathrm dt}

Integrating both sides gives

V_C = -\frac{k_1M}{C_f}a

And it can be found that

\begin{align*} V_\text{out} &= -A_{OL}(V_\text{out} - V_C) \ V_C &= -V\text{out} \frac{1+A_\text{OL}}{A_{OL}} \end{align*}

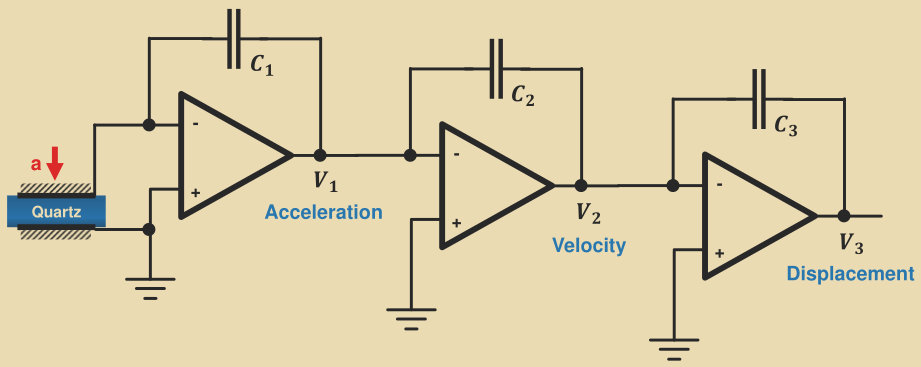
To get

V_\text{out} = \frac{k_1M}{C_f}a

This circuit can be stacked to get velocity and displacement: